关于SIFT算法中降采样与sigma的研究

摘要

之前在SIFT算法中，有一个加速操作是使用图像金字塔，即不断对图像进行降采样。按照算法的思想表明：降采样后，标准差为$\sigma$的高斯模糊图像标准差会减半，得到标准差为$1/2\sigma$的高斯模糊图像。

这里我不知道该如何证明....网上也没有相关资料，所以暂时采用数值解去验证这个说法。

实验过程

代码贴在最后，主要思路是比较两张图像：一张是先降采样一倍再用$\sigma$高斯模糊的图像；另一张是先使用$2\sigma$进行高斯模糊，再在模糊的图像上进行一倍降采样。

首先可视化这两张图，肉眼查看之间的差距，确实差距还是挺小的。此处$\sigma=30$（忽略窗口的值，那里标错了~）

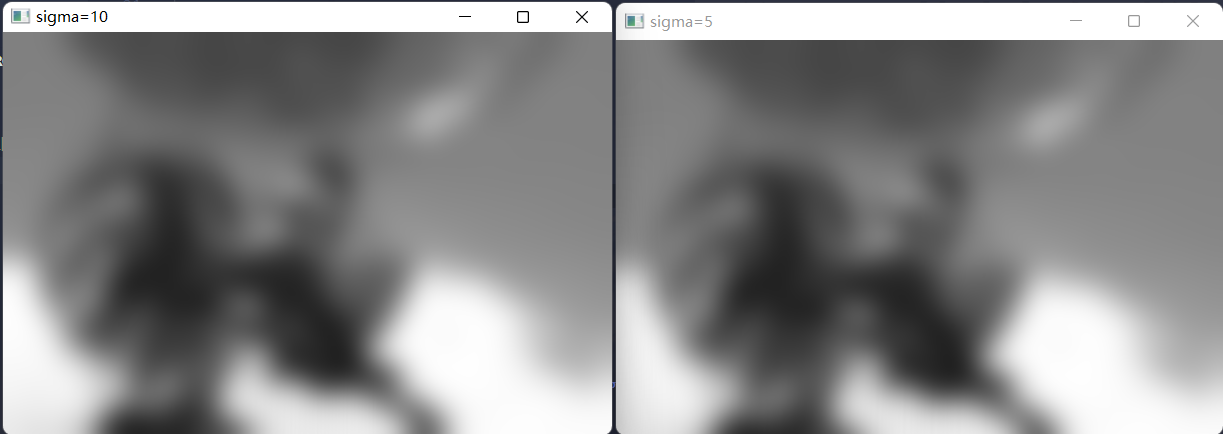
为了对比，这里把原图分别使用$\sigma$和$2\sigma$进行高斯模糊的结果也可视化了出来。这两张图就明显存在差异,这说明对高斯模糊过的图像降采样，确实会对其$sigma$产生影响。

接着最早的两张图做差并画出来，可以看到形成了一个类似边缘检测的图像。这说明“先降采样再$\sigma$高斯模糊”跟“先$2\sigma$高斯模糊再降采样”这两个操作不完全等价。

为什么看上去是边缘检测图像？其实也很好理解，对于不同$\sigma$的高斯模糊图像相减，就是对高斯模糊图像微分，即DOG，DOG和LOG又只差一个常数倍，所以等效边缘检测了~

接下来再探究“先$2\sigma$高斯模糊再降采样”得到的模糊图像的标准差到底是多少。最暴力的方式就是搜索，我们在降采样的图像上使用不同的$\sigma$进行遍历，画出delta的范数变化情况。最后我们发现：最接近的$\sigma_0$就是$\sigma$!

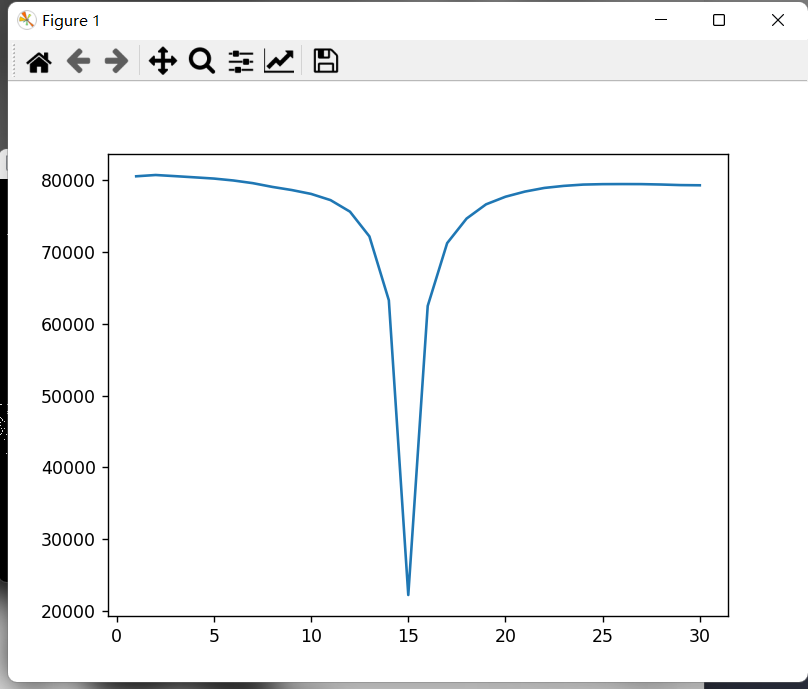
至此，我们知道上述的两个操作并不等价，但是它们足够接近。所以SIFT算法通过这种近似去做图像金字塔，大幅提高运算效率。

代码

import cv2

Path = "C:\\Users\\Axuanz\\Desktop\\download.png"

if __name__ == "__main__":
    img = cv2.imread(Path,cv2.IMREAD_GRAYSCALE)

    sigma = 30

    ksize1 = sigma*6+1
    ksize2 = int(sigma/2*6+1)

    blur1 = cv2.GaussianBlur(img,ksize=(ksize1,ksize1),sigmaX=sigma)
    blur1 = cv2.pyrDown(blur1)

    downsample_img = cv2.pyrDown(img)
    blur2 = cv2.GaussianBlur(downsample_img,ksize=(ksize2,ksize2),sigmaX=sigma/2)

    blur3 = cv2.GaussianBlur(img,ksize=(ksize1,ksize1),sigmaX=sigma)
    blur4 = cv2.GaussianBlur(img,ksize=(ksize2,ksize2),sigmaX=sigma/2)

    delta = blur2 - blur1
    print(cv2.norm(delta))

    cv2.imshow("sigma=10",blur1)
    cv2.imshow("sigma=5",blur2)
    cv2.imshow("blur3",blur3)
    cv2.imshow("blur4",blur4)
    cv2.imshow("delta",delta)
    # cv2.waitKey()

###########################################
    sigma2 = 1
    norm_list = []
    while sigma2 <= sigma:
        _ksize = sigma2*6 + 1
        blur = cv2.GaussianBlur(downsample_img,ksize=(_ksize,_ksize),sigmaX = sigma2)
        delta = blur - blur1

        norm = cv2.norm(delta)
        print(f"sigma2 = {sigma2},delta norm ={norm}")

        norm_list.append(norm)
        sigma2 += 1

    import matplotlib.pyplot as plt
    x = list(range(1,sigma+1))
    print(x)
    print(norm_list)
    plt.plot(x,norm_list)
    plt.show()
###########################################