摘要
SVM是神经网络兴起之前最常用的机器学习分类器,本篇主要介绍SVM的具体实现,包括硬间隔/软间隔、合页损失函数。PPT参考https://www.bilibili.com/video/BV1zq4y1g74J/?spm_id_from=333.788&vd_source=6e11e901eb83e70a9bb55225ac28b9d9
SVM推导
SVM一般用于解决数据的二分类问题,对于高维数据,就是找到一个超平面将两类数据分开。以二维平面为例,就是找到一条直线作为分割线。
当然有时候我们无法找到理想直线将两类数据分离,这个时候就需要用到非线性SVM,通过核函数将数据点映射到高维空间,以期望在高维空间找到一个超平面分离数据。
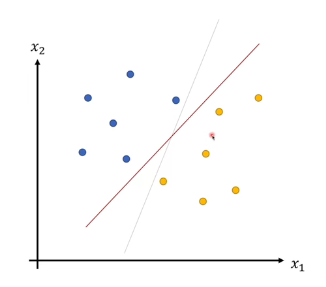
SVM的思想不仅是找到一个分割直线,它还希望这条直线离两类数据都尽可能远,也就是最大小下图中的$margin$。
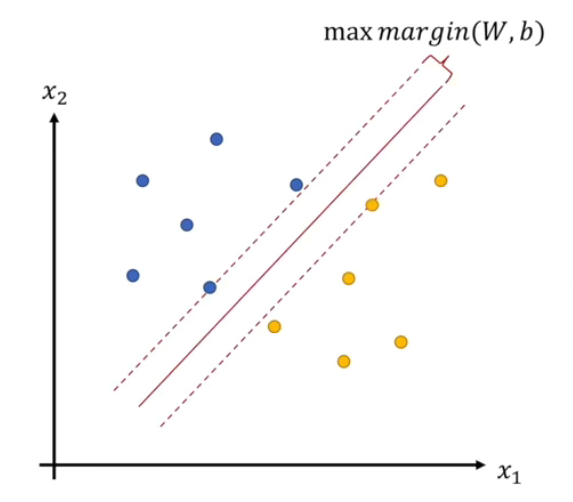
$margin(W,b)$与直线参数$W,b$有关,形式化表示可以写成:
$$
max \space margin(W,b)=max\mathop{min}\limits_{i=1,2,...N} \frac{1}{||W||_2}|W^TX^{(i)}+b|
$$
$margin$的表达式为什么是直接将数据点$X^{(i)}$带入直线(高维数据时其实是超平面,但是为了描述方便之后都用直线方程替代)方程然后除以W的L2范数?推导如下,首先写出某个数据点到直线的距离方程,距离可以表达成W和数据点向量之间的点积除以W的模。假设$x^{(0)}$是平面上的一点(所以$W^TX^{(0)}+b=0$),那么距离H就可以表示为:
$$
\begin{aligned}
H &= |\frac{W}{||W||_2}(X^{(i)}-X^{(0)})|\\
&= |\frac{1}{||W||_2}(W^TX^{(i)}-W^TX^{(0)})|\\
&= |\frac{1}{||W||_2}(W^TX^{(i)}+b)|
\end{aligned}
$$

除了满足最大$margin$外,我们还希望这个超平面可以正确分割数据点,我们将数据点的标签标为1或-1,那么如果直线可以正确分类,那么满足以下两个条件:

进一步将优化问题转变成以下条件:

为了简化问题,我们将离直线最近的数据点$X^{(i)}$离直线的距离$|(W^TX^{(i)}+b)|$约束到1,那么优化问题就变成了下图,并且添加了一个约束条件。之所以可以这么优化,是因为对于原来的$margin$,$W,b$同时扩大N倍,都不会影响margin的结果,所以这里可以扩大(缩小)两者的值,使$|(W^TX^{(i)}+b)|$约束到1,从而简化问题。
注意,这里的$X^{(i)}$是离直线最近的那个数据点,所以可以把$margin$的min脱掉

合并约束条件得到以下优化条件:

将max转换成min,得到:

进一步写成矩阵相乘的形式,并通过拉格朗日乘子法优化,这里约束条件是不等式,满足KKT条件。数据点在边界上时$\lambda$不等于0,存在约束;如果不在边界上则不存在约束。具体可查阅KKT条件相关知识。
这里引入1/2不会影响结果,但是可以方便之后的求导运算

对上图中的L求导,得到最优解。此时W可以表示为边界上各个数据点的线性组合,这些数据点$X^{(j)}$就被称为支持向量。

SVM的损失函数
我们回过头看SVM需要优化的那个拉格朗日函数,其实它和神经网络中的损失函数很像,第一项相当于W的L2正则化项,第二项则是”损失函数“。

上述的SVM是硬间隔SVM,因为它的损失函数要求SVM直线对于每个数据点都分类正确,然而实际上会出现不可分的情况。那么这个时候就需要对优化函数进行修正,从而得到软间隔SVM。

通过添加$\xi$,使约束条件放开。同时也将$\xi$的常数倍加入损失函数优化,从而尽可能找到一个小的间隔$\xi$。

合并约束条件,我们可以得到以下结果。这个时候我们已经可以看到Hinge loss的身影了。

把约束项合并到损失函数中,就可以得到软间隔SVM最终的损失函数形态。第一项是损失函数,第二项是W的正则化项。

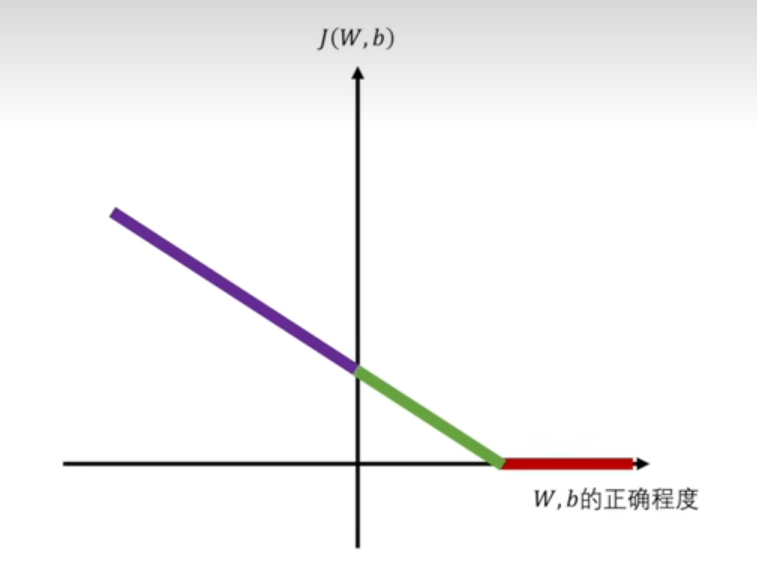
而第一项就是我们熟知的Hinge Loss,合页损失函数。

评论
🐂