摘要
语义分割任务是将一张图像做像素级别的分割,将一些原始数据(例如平面图像)作为输入并将它们转换为具有突出显示的感兴趣区域的掩模。它的难度会比图像分类和物体识别更难。当然我们这里讨论的分割效果还是从像素的一些统计特征出发,并没有引入人的先验认知知识(其实也多少引入了一点,例如格式塔理论,不过基于这个理论的算法难以建模),所以效果是比较差的。
格式塔理论
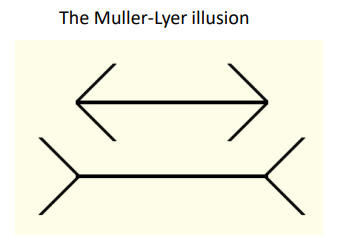
格式塔理论其实是一种心理学理论,它表明人类视觉是整体的:我们的视觉系统自动对视觉输入构建结构,并在神经系统层面上感知形状、图形和物体,而不是只看到互不相连的边、线和区域。最经典的问题就是比较线段长短。
格式塔理论给我们了一些设计语义分割的思路,它给出了一些像素点分类的指导思想。例如通过地理位置、相似性、平行、对称等关系去分类像素点,实现分割。
这里其实就是自底向上的分割思路。人类看到一张图像做分割,应该是根据已有的知识,自顶向下地去分离物品,比如从人的分离、再到人身上衣服、首饰的分离;而机器做分割,都是从像素出发做分割,单从像素点没办法理解分割操作,这就需要格式塔理论给出的一些人眼视觉的底层模式来指导自底向上的分割了。
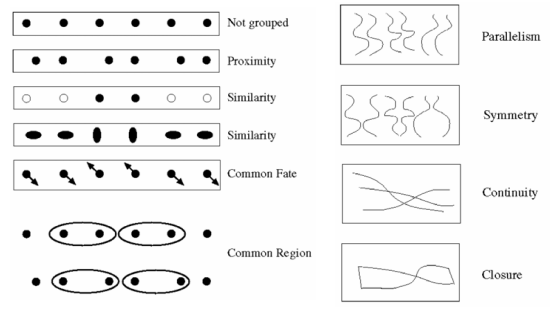
实际上,格式塔理论给出的这些模式虽然符合人的视觉特性,但是用算法难以建模。所以只有一部分模式被用在算法中。
基于聚类的分割
分割最简单的一个方法就是聚类,通过将相似的像素点聚在一起,将其认为是一个分割块,最终聚类的分类结果就是分割结果。聚类采用的特征可以是简单的RGB值,也可以是带有位置信息的RGB值,当然也可以是灰度值。
以下是不加入位置信息的灰度图、RGB图的聚类结果。可以发现这种分割并不能分割不同实例,比如两个辣椒连同西兰花都被聚在了一起。

如果加入位置信息,不同实例由于空间位置不同,就有可能被区分,例如下图的两个黄瓜片。

聚类的方式有很多,常见的就是KMeans。具体算法及其优缺点可以参考之前的博客~
Mean shift聚类与分割
先看两张Mean shift做分割的两张结果,还是挺惊艳的。
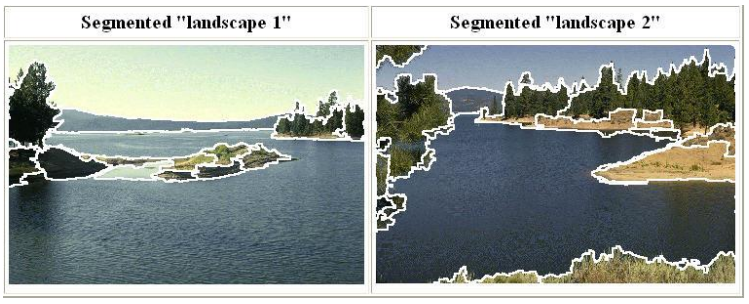
总的来说,Mean shift有点像基于密度的算法(例如DBSCAN这种),它是计算给定圆框的重心位置,不断让圆框的圆心逼近重心的方向,从而找到密度最大的那个点。在这个过程中,圆框框住的那些数据点,都可以理解是同一个类。给两张图感受一下就懂了。
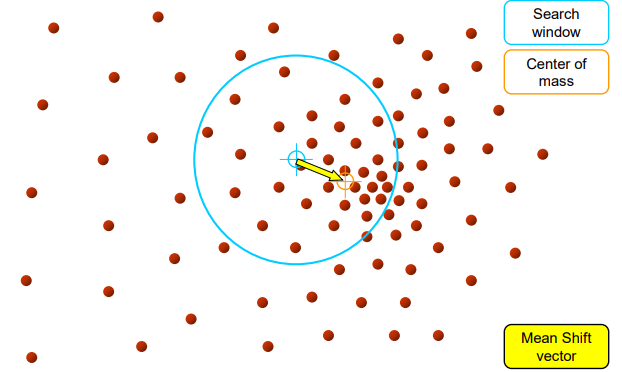

算法思想是比较简单的,就是找到一张图像的多个密度中心,每个密度中心认为是一个类。当然为了提高效率,算法还做了一些trick,比如label扩散等等。
Mean Shift有以下优缺点
优点:
- 不用假定数据簇的形状(因为基于密度)
- 只需要一个简单参数,即圆窗的大小
- 可以找到不同的模式(因为只依赖数据点密度)
- 对于外点鲁棒
缺点:
- 效果取决于圆窗大小
- 计算量比较大
- 无法对付高维特征(之前在KMeans也提到过,就是高维灾难,数据点在高维空间是稀疏的,通过密度不好迭代)
图论分割
图论分割的思想是:把图像认为是一个图G(V;E),首先计算相邻像素点之间的距离Dis,再通过Dis为图中的每条边建模相似度Similarity,然后找到一个最小cost的切割,将整张图切成两份,完成二分类的切割,重复多次就完成语义的分割。

具体例子如下,边的权值代表相似度。
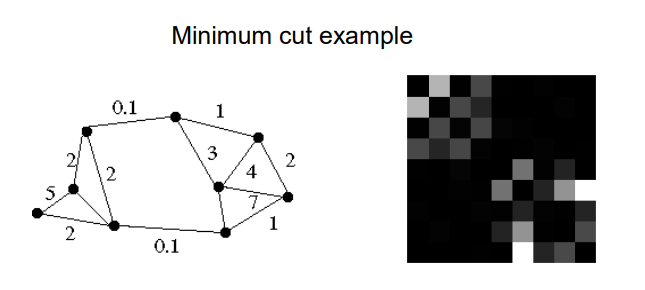
找到一个最小分割,就把最不相似的两份数据点分离开。
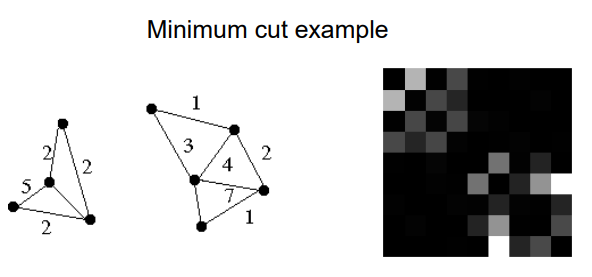
当然如果只找最小cost的切割,容易出现孤立点的情况。
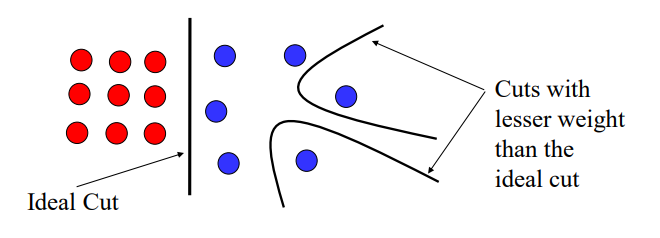
所以引入图论中的正则化切割,将cost重新建模为
$$
cost = \frac {w(A,B)}{w(A,V)} + \frac {w(A,B)}{w(B,V)}
$$
最终计算最小切割的流程如下:
- 计算W矩阵,即邻接矩阵,代表任意两点之间的相似度
- 计算D矩阵,D矩阵为对角矩阵,对角内容为W矩阵对应行的和
- 最小正则化损失表示为下式,其中y是01向量,代表图中数据点的分类情况
$$
normalized-cost=\frac {y^T(D-W)y}{y^TDy}
$$
- 接下来求上式最小值,可以转换成求解以下方程$(D-W)y=\lambda Dy$,进一步转换成$D^{-1}(D-W)y=\lambda y$,即求$D^{-1}(D-W)$矩阵的倒数第二小特征值(因为矩阵有最小特征值0),对应的特征向量y就是结果。
纹理特征聚类进行分割
我们也可以使用之前提到的纹理特征提取图像信息,再通过聚类将相似的像素点聚在一起,达到分割的目的。

不过纹理特征聚类这种方法在边缘表现不好,会将一个物体的边缘部分也作为一个实体。


评论