摘要
本节主要介绍尺度不变特征以及其经典代表——SIFT,网上关于如何计算SIFT特征的博客有很多,但是大多数博客都没有解释为什么这样找到的特征就是"尺度不变"的、为什么尺度和$\sigma$相关联等问题。因此这篇博客会对这些问题进行一些个人的补充,不一定对,欢迎留言~
尺度不变特征
在这里,我想把尺度理解成某个物体的大小。那么尺度不变特征就可以解释为:那些随着物体尺度变化而不会发生改变的特征。
具体来说,可以假设两张都有一个黑色实心圆的图片,图片大小保持一致,而图中的圆半径不一致。圆的尺度不同,那么尺度不变特征就可以理解成这两张图中共有的一些特征,这些特征不会随圆的改变而变化/消失。当然这里的圆也可以是复杂的建筑,如下图所示。
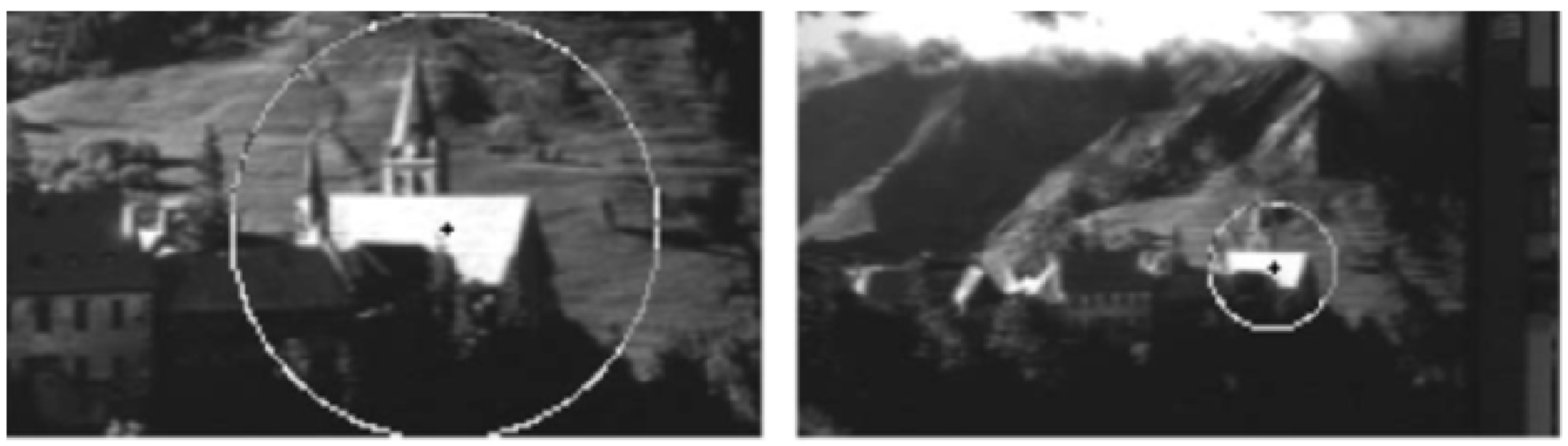
之前提到的harris角点就明显不是一个尺度不变特征,当角点的大小放大到一定程度,只能检测到边,而检测不到角点,这说明角点特征不是尺度不变的。
回到刚刚圆的例子,我们希望能有一个特征,可以描述不同半径的圆。如果找到了,那么我们就可以允许识别任务中摄像头可以有一定的远近变化,这是非常有意义的,因为生活中的大部分识别任务不能100%保证摄像头与物体始终保持固定的距离。这就是尺度不变特征的意义。
拉普拉斯模板与圆形检测
之前介绍过高斯偏导模板,高斯一阶导模板可以检测边缘(边缘点的响应结果为极值),二阶导同样可以做到(边缘点的响应是0),我们称高斯二阶导模板为拉普拉斯模板。
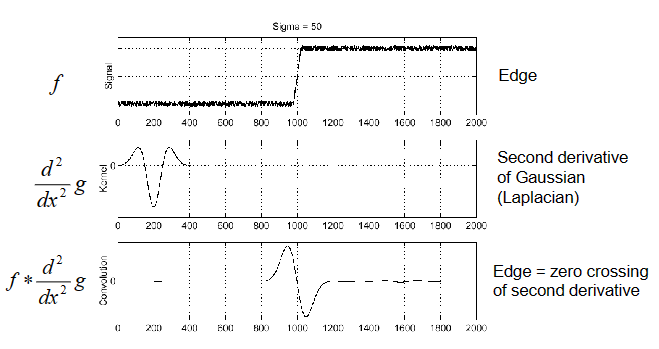
拉普拉斯模板有个特点:对于特定宽度的信号,存在某个$\sigma$的拉普拉斯模板,两者卷积结果响应具有最大值,如下图所示。换句话说,对于某个宽度的信号,都可以找到一个$\sigma_0$对应的拉普拉斯模板,使两者在信号中间那个点的响应$f_0$最大,并且其他$\sigma$的拉普拉斯响应都小于$f_0$。
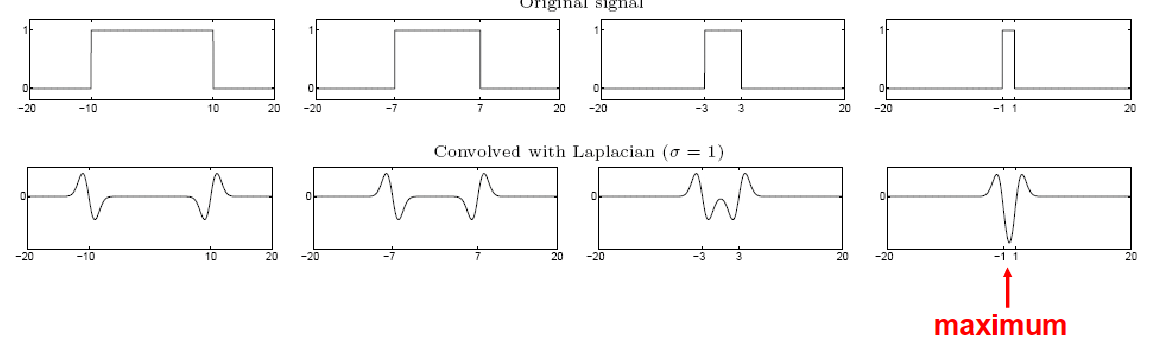
那么这个响应什么时候最大呢?可以证明:当信号宽度和拉普拉斯模板的0平面宽度一致时,响应可以取到最大值。带入拉普拉斯模板零平面方程可以得到$\sigma=r/\sqrt2$。
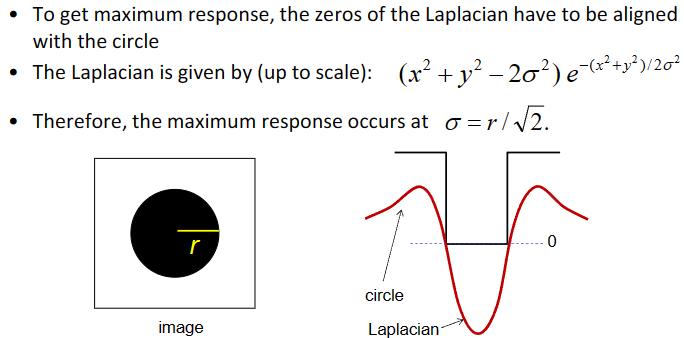
至此,我们发现拉普拉斯模板可以检测圆形物体,具体方法是:对于同一张图像,我们使用不同的拉普拉斯模板去卷积($\sigma不断增大$),得到一系列卷积响应图。对于每个像素点,我们取出这些相应图中对应位置的响应,组成一个响应值序列。如果该序列存在极值,即满足响应从小到大再到小的趋势。那么我们可以认为在这个像素点可能是一个圆的圆心,圆的半径就是响应极值对应的拉普拉斯模板的$\sigma$乘以$\sqrt2$。
尺度与sigma
以上说明还没有涉及尺度不变的问题,现在我们回到最开始提到的两张图像,两张图象都有一个圆,圆的半径不同。对于其中一张图像,我们通过上述方法可以检测出圆形的位置和大小。对于另外一张呢?同样可以!两者的区别只在于,我们通过一系列拉普拉斯模板去寻找响应值极值时,两张图片极值出现的像素点可能不同(圆心不同)以及极值对应的拉普拉斯模板$\sigma$不同(半径不同)。
但是这背后蕴藏了一个信息:对于圆这个物体,我们通过拉普拉斯响应可以在不同图像中都识别到它。并且这个圆大小并不影响我们的检测,无非是寻找到的$\sigma$不同而已。
那么这种拉普拉斯极值响应,是不是就是一种尺度不变的特征呢?答案我认为是对的,事实上这就是SIFT特征的理论基础。
还有一个小问题:我们刚刚发现拉普拉斯响应极值对应的$\sigma$和最终检测出来的圆形半径有关,圆形半径越大,$\sigma$越大,对应的拉普拉斯响应图越模糊。所以我们可以将圆形大小、$\sigma$、卷积结果的模糊程度联系起来。并且也多少能够解释网上的这种说法:不同$\sigma$的高斯模板卷积出来的图片对应不同的尺度空间,尺度原本应该描述大小上的关系(至少我的第一反应是),实际上却和图片的模糊程度相关。
SIFT特征
关于SIFT特征的求法,网上的资料已经非常丰富了。这里大概提一下重要的几个点。
改进一
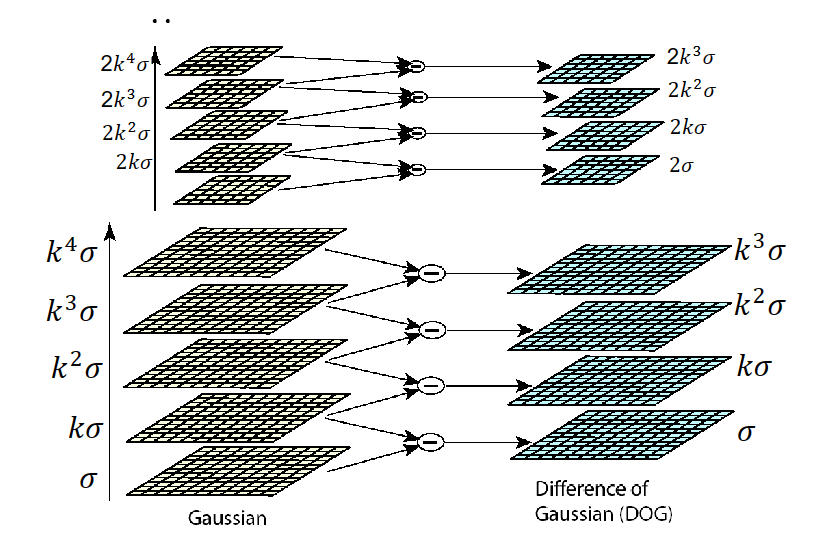
第一个改进是使用DOG近似LOG,这是利用高斯模板之间的差分来近似拉普拉斯模板。可以证明的是
$$
normed \space LOG = \sigma \frac{ \partial G }{ \partial \sigma }
$$
$$
G(x,y,k\sigma) - G(x,y,\sigma) \approx (k-1)\sigma^2 \nabla ^2G
$$
那么我们就可以通过DOG(Difference of Gaussians)去近似LOG,可以节约计算量~
改进二
其次是不同$\sigma$的高斯响应,我们使用不同$\sigma$的高斯模板对于原图进行多次卷积操作。事实上,随着sigma不断增大,卷积核也越来越大,计算效率会不断降低。所以为了节约效率,SIFT有了第二个改进,通过上一次卷积的结果计算下一次卷积,这里用到了卷积的可加性,如下所示。
$$
\sigma_{op} = \sqrt{\sigma_{next}^2-\sigma_{curr}^2}
$$
我们要得到一个$\sigma_{next}$的结果,只需要在$\sigma_{curr}$的基础上做一次$\sigma_{op}$的卷积就可以了。
改进三
第三个改进是使用多尺度的响应图,不同octave之间的图像大小相差一倍(使用上一个octave的倒数第三张图片缩放一倍后作为本octave的第一张图片,并且第一张图片不再做高斯模糊处理,为什么是倒数第三章可以参考其他博客,大概就是这种$\sigma$分布可以保证倒数第三张的$\sigma$刚好是$k\sigma$)。这里同样是考虑运算效率,小图上的卷积更快,并且降采样可以视为$sigma减半$,意味着不同octave之间可以使用相同的卷积模板,这也是opencv实现中的一个trick。
改进四
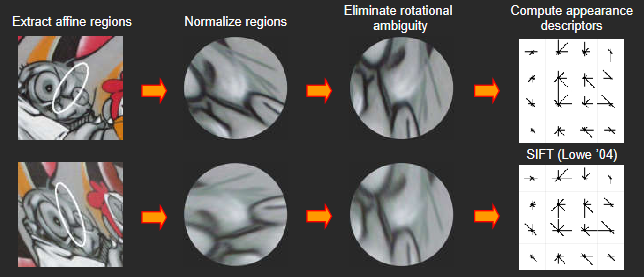
由于原始SIFT只能检测出圆形的特征区域,无法克服拍摄视角等问题。所以可以使用放射变换对圆进行微调。

具体用到了之前harris角点提到的M矩阵,通过改变圆某个方向的半径,使M矩阵的两个特征值尽可能保持一致。具体方法就是,首先通过R矩阵确定圆形拍扁(拉长)的方向,在特征值较小的方向,将检测出来的圆进行压缩,直到椭圆区域内的M矩阵两个特征值一致。

改进五
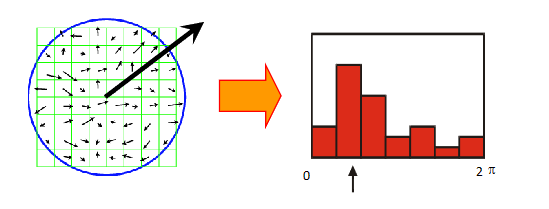
对于提取出来的区域,我们可能会遇到视角旋转等问题。所以这里需要对提取出来的区域做一次归一化旋转。具体来说,就是统计区域内的各个像素点的梯度方向,画出统计直方图,根据直方图的主方向进行旋转,达成归一化的效果。因为只涉及梯度,所以这种方法对于光照、环境都是鲁棒的。
SIFT描述符
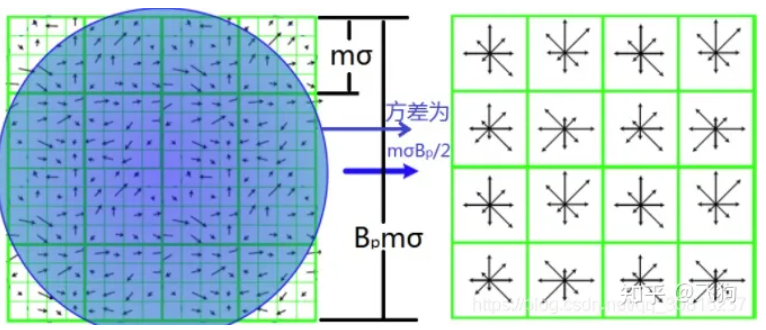
SIFT描述符的生成网上有很多资料,大致就是把SIFT区域分成4x4的子区域,每个子区域统计8个方向的梯度方向直方图,通过这八个实数来描述这个子区域,因此最终一个区域可以得到大小为128维的SIFT向量。这就是SIFT描述符了~
总结
总的来说,SIFT特征理解起来还是比较抽象的,特别是尺度不变部分的描述。SIFT描述符也不止用在SIFT算法中,只要是对某个区域进行特征抽象都可以使用SIFT描述符的思想。

评论
写的很好!硕导加油!早日评上院士