摘要
特征提取是视觉中的一个重要任务,通过提取特征点,可以完成全景拼接等操作。harris角点就是一个比较好的特征。
特征选择
一个好的特征具有以下几种性质。
- 重复性,特征在不同摄影角度、不同地理位置得到的一系列照片中都应该出现。
- 特殊性,特征应该是特别的,容易辨认的。
- 计算友好,提取特征需要考虑计算效率。
- 局部性,特征应该占据图像的一小部分,对杂波和遮挡具有鲁棒性
特征点应用
特征点应用可以用在图像对齐、3D重建等等视觉任务。

角点
在角点周围的区域中,图像梯度具有两个或多个主导方向,并且它具有重复性、辨别度高。所以角点是一个比较好的特征。
识别角点可以使用一个方框,当方框框住角点时,往任意方向移动,方框内的内容都会发生改变。
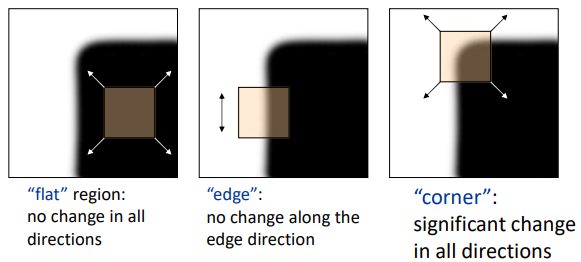
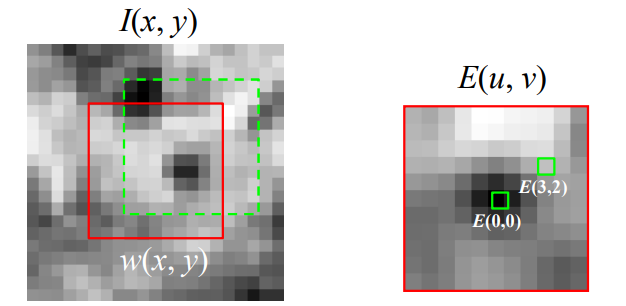
我们可以使用$E(u,v)$来描述一个方框移动时,方框内容的变化程度。这里的I指图像强度,也是像素值大小。$x,y$指方框内的各个像素点的坐标.$w(x,y)$指不同像素点的权重,一般方框中心的权重较大。
这里的E(u,v)是相对于某个固定位置的方框定义的,其实可以表示成$E(X,Y,u,v)$,$X,Y$是方框中心点位置,因为之后要用到不同位置的E
$$
E(u,v) = \sum_{x,y}w(x,y)[I(x+u,y+v)-I(x,y)]^2
$$
原始的$E$计算过于复杂,每次都需要取方框内和移动后方框内的像素值进行计算。所以这里使用二维二阶泰勒公式进行近似。这里在(0,0)处展开,也就是麦克劳林展开。
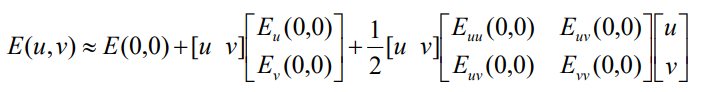
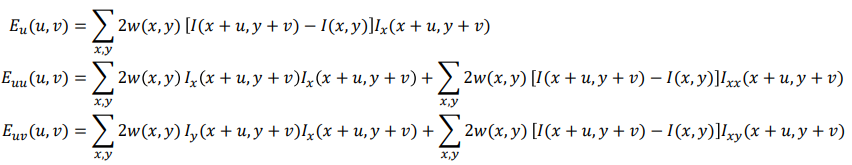
最后得到结果如下图。$E(u,v)$变成$M$矩阵的二次型,而$M$矩阵是二阶黑塞矩阵。这里假设I是二阶连续可导的,所以$I_xI_y=I_yI_x$。
这里x,y应该是指u,v,表示偏导的第一个参数和第二个参数。
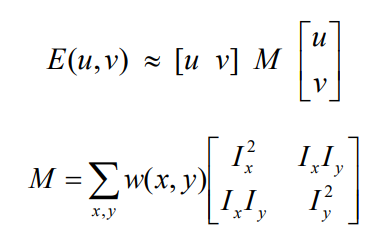
现在回顾一下角点的性质,对于框住角点的方框。无论是u方向还是v方向,$E(u,v)$都具有较大值。
而$M$矩阵是实对称矩阵,具有n个正交的特征向量,因此可以相似对角化。R是正交矩阵,所以也可以理解成旋转矩阵,可以对坐标进行旋转映射。
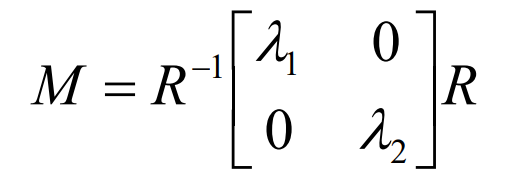
先不考虑R的影响,当M是对角矩阵时,只有两个特征值都不为0时,$E(u,v)$才是$u,v$的函数,表示$E$在$u,v$方向都敏感。假如$\lambda_1=0$,那么$E$对于u不敏感,那么这个方框的中心点应该在一条线上。
这个时候考虑R,其实也只是对于移动量$[u,v]$进行坐标的旋转。不影响结果的判断。可视化来说,$M$分解得到的R其实就是负责旋转角点与坐标轴对齐。
harris角点总结
综上所述,判断一个像素点是否是角点。首先构建这个像素点的$E(u,v)$函数,再根据泰勒展开进行化简,得到M矩阵,根据M矩阵的特征值可以得到该像素点的$E(u,v)$随着$u,v$的变化趋势,从而判断该点是否是角点。
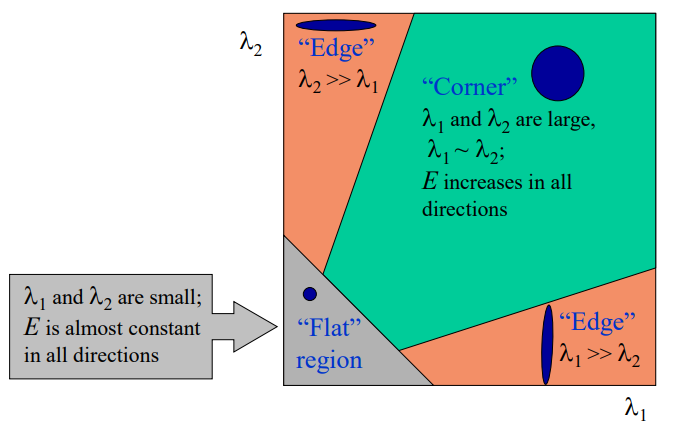
实际应用时,可以通过以下公式化简,不需要计算矩阵M的特征值。
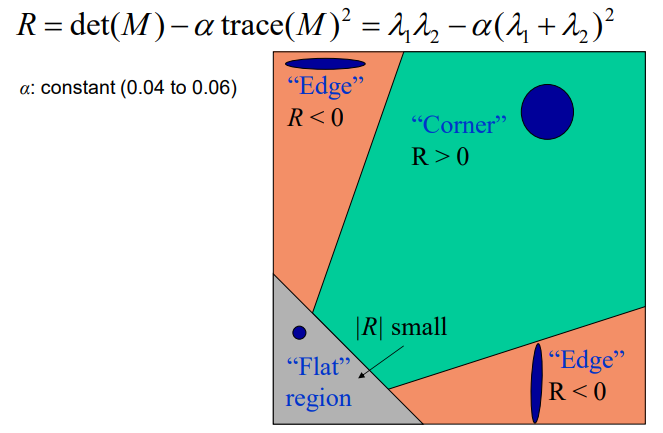
harris角点的形式化流程如下。
- 首先通过高斯偏导模板获得每个像素的方向导数
- 计算每个像素的矩阵M
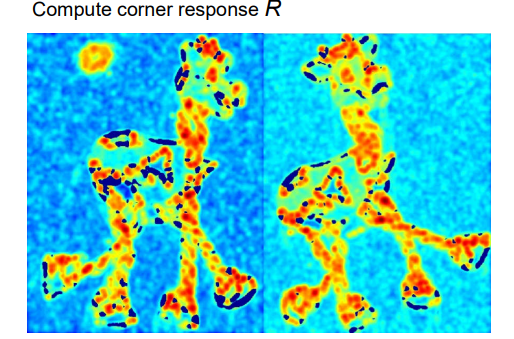
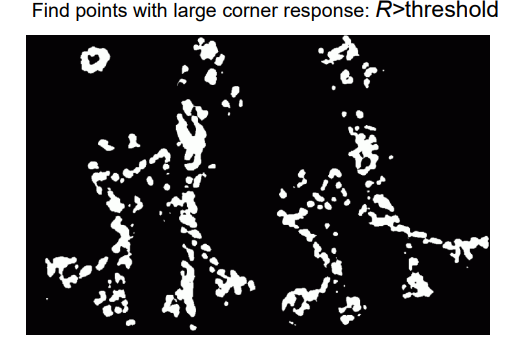
- 通过判别式计算R值,再根据阈值判断是否是角点
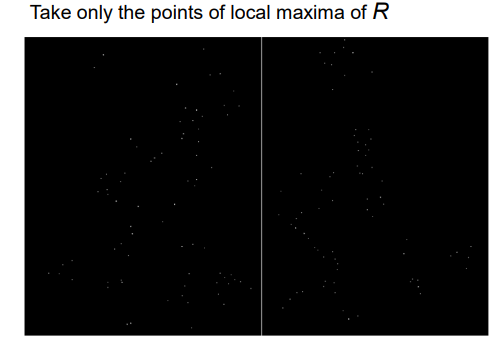
- 为了减小角点个数,使用NMS极大值抑制
完整检测过程如下图。

Invariance and covariance
Invariance:
- $feature(transform(image)) = features(image)$
Covariant:
- $features(transform(image))=transformorm(features(images))$
harris角点算法对于位置和旋转是Covariant,但是对于尺度放缩不是Covariant

评论