摘要
Hough变换相比于其他的拟合方法,它可以检测多个图形(当然RANSAC采用TOPK也可以实现多图形检测)。具体来说,Hough变换是将图像空间的像素点向参数空间投影并投票,通过投票最大值得到最优参数。
直线拟合
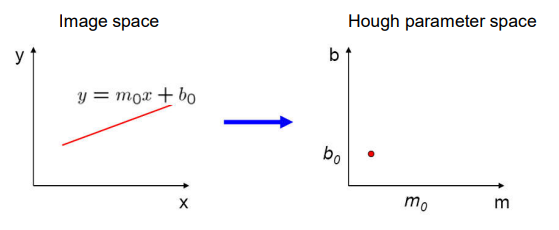
二维空间的直线有两个参数$m,b$。那么Hough变换投影的参数空间也是二维。
对于图像中的一条线,对应参数空间中的一个点,该点的票数加一。
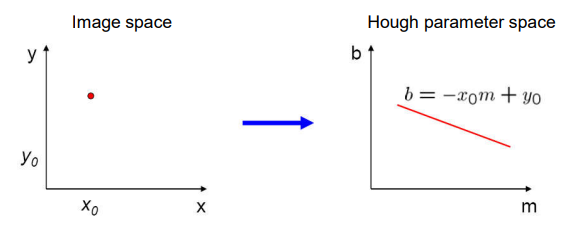
对于图像中的一个点,对应参数空间中的一条线,线上的票数加一。
那么对于图像中的多个点,如果这些点有较好的线性关系,那么参数空间投票时,会有一个点票数最高,而这个点则是拟合直线的参数。
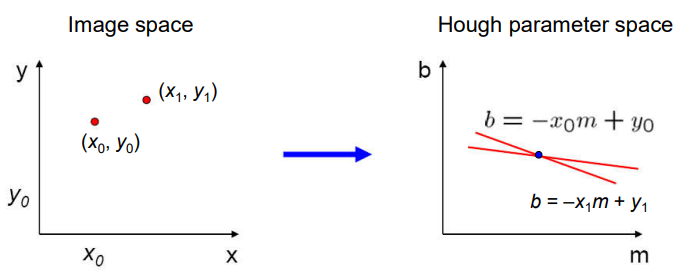
上述参数空间有个问题,就是$m,b$的范围无法确定,如果直线垂直x轴,m会趋于无限大,参数空间也趋于无限大。因此需要换一种参数表示,这里使用极坐标表示直线。
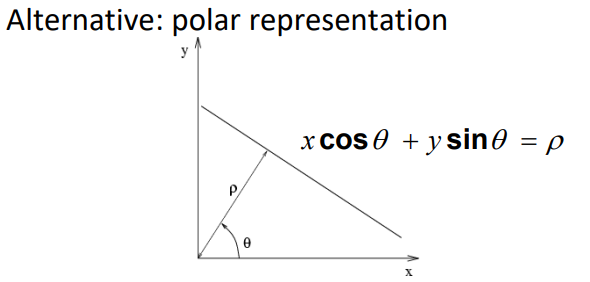
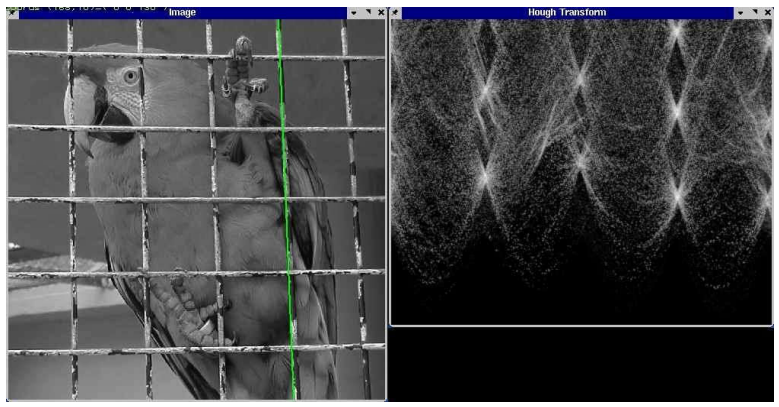
更换坐标系后,投票策略转换为下图。对于图像上的每个点(这里说图像一般是指边缘图像,可以是canny算法得到的结果),根据已知$x,y$,遍历$\theta$值,得到对应$\rho$,参数空间中的网格加一票。最后选择票数最高的作为拟合结果。

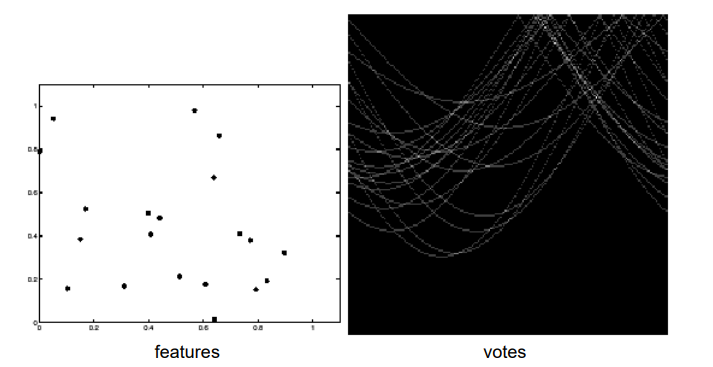
直线拟合效果如下,右侧为参数空间,亮度代表票数。
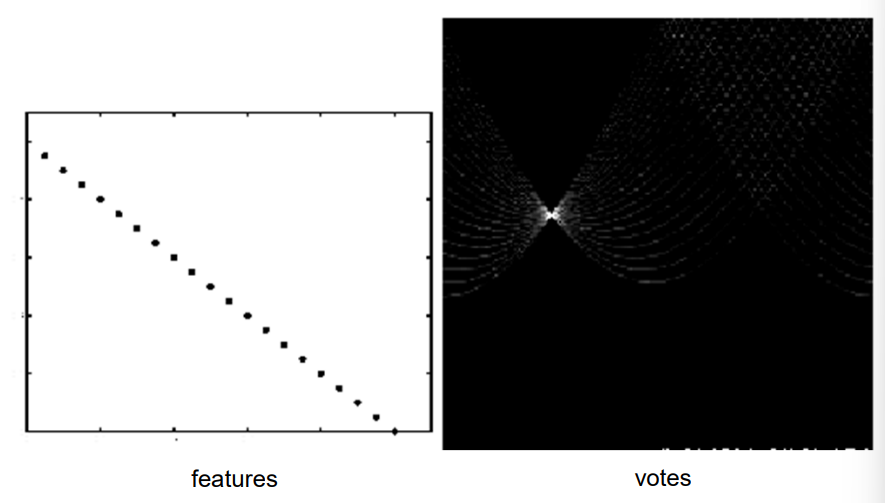
方形和圆形拟合结果如下。
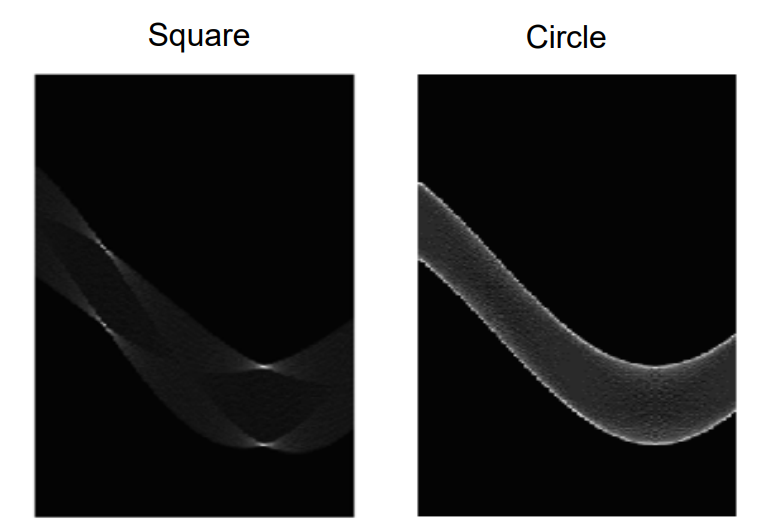
噪声影响
如果往数据点中掺入随机高斯噪声,那么参数空间中的亮点会分散。单个参数网格对应的票数会减小。
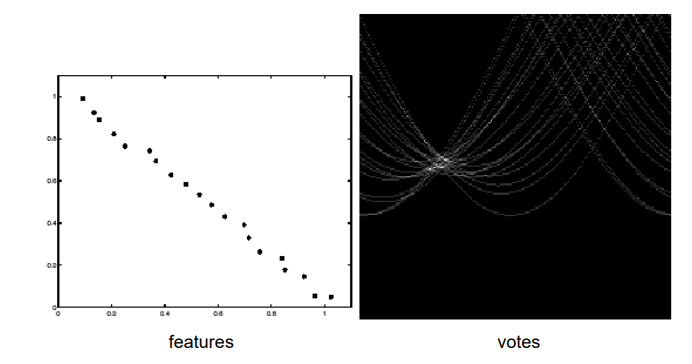
关于处理噪声点,有以下几种方法:
- 选择适合的网格大小。如果网格太大的话,一个网格代表多条直线,拟合结果不准确;网格太小,每个网格的票数较少,如果无法达到阈值,则无法检测
- 使用软投票。给网格投票时,依据高斯分布给附近的网格也投票。
- 不适用无关的特征。通过canny算法预先处理图像边缘,可以得到图像每个边缘点的梯度大小和方向,该点的边缘线与梯度方向垂直,那么给参数空间投票时,只需要给固定的$\theta$方向投票即可!
随机点影响
对于随机的数据点,参数空间也可能出现票数较高的网格,造成错误拟合。
参数搜索优化
刚刚提到:使用canny算法预先处理图像边缘,可以得到图像每个边缘点的梯度大小和方向,该点的边缘线与梯度方向垂直,那么给参数空间投票时,只需要给固定的$\theta$方向投票即可。投票算法如下图。

这里的$\theta$正好和梯度的方向$\theta_2$一致,都与边缘线垂直。
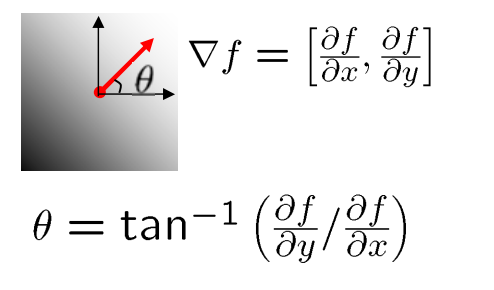
拟合圆形
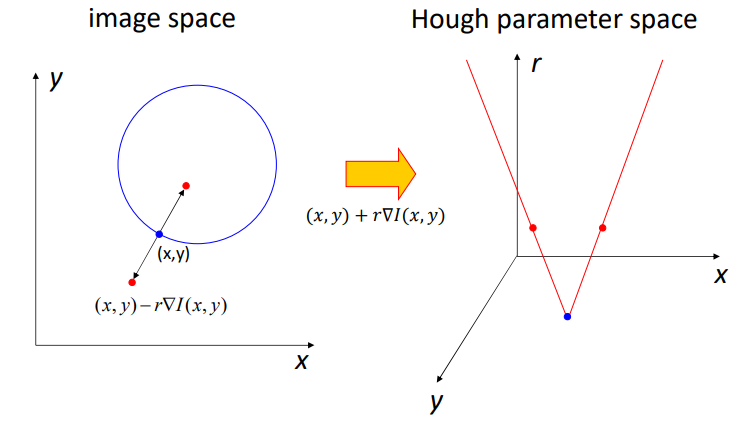
圆形有三个参数,$x,y,r$,所以参数空间是三维的。对于一个数据点,确定该点梯度方向后,圆心可能出现在两个地方,然后再枚举r,并在参数空间里的小方块里投票。这里r是有界的,最大不超过图像的大小。
如果不使用梯度方向进行优化,那么圆心可能出现在数据点为圆心的一个圆上,参数空间投票可视化也就是一个圆锥。计算量会很大。
这种方法对于尺度放缩和嘈杂环境是鲁棒的。

泛化使用Hough变换
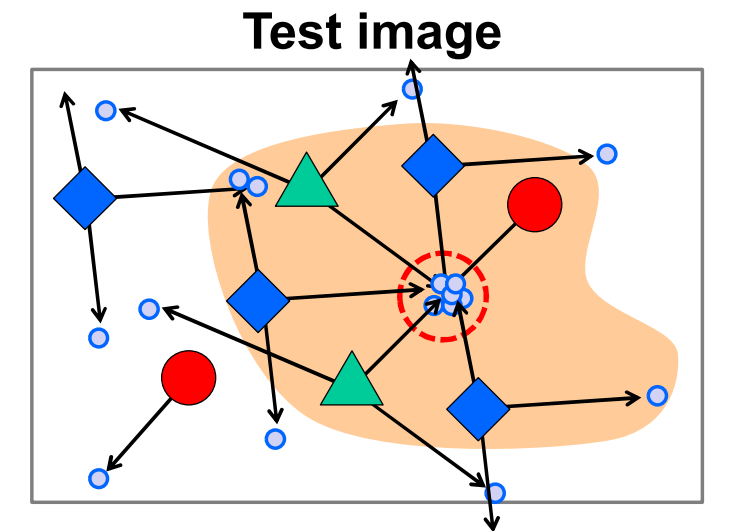
Hough变换还可以用来识别物体中心点。给定每种元素的分布和图形中心点,可以画出每种元素的矢量图。
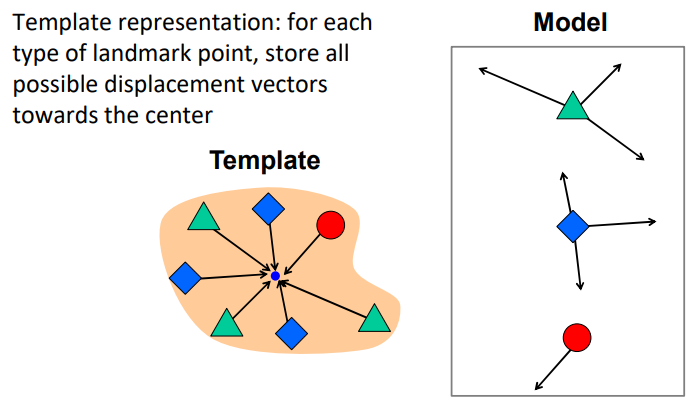
测试时将图中的每个元素都套用矢量图,根据投票最多的点可以确定图形中心点。

总结


评论