摘要
如果说边缘检测只是将给定图像的边缘提取出来,那么拟合就是对这些边缘进行数学建模,得到形式化的数学表示。接下来以最简单的拟合直线为例。
最小二乘法
损失函数是所有数据点拟合直线的预测值与真实值的差的平方和。
可以通过偏导或线代的向量投影得到最优参数,下图为偏导过程与结果。

全最小二乘
最小二乘有两个问题:首先是无法表示垂直x轴的直线,二是损失函数不能很好表示直线与数据点之间的距离。全最小二乘对此进行了改善,首先修改了直线的表示方式,其次损失函数从纵向距离改为了直线到数据点的垂直距离。

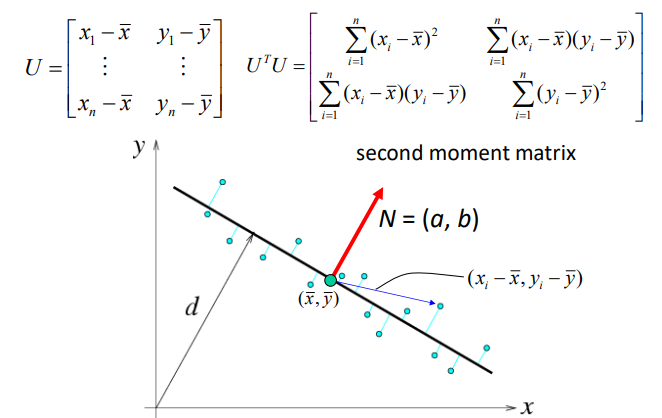
求解步骤是:首先通过E对d偏导,得到d的a,b参数表示;再找到$U^TU$矩阵的最小特征值,对应的特征向量就是参数a,b的值(最好情况就是找到特征值0的特征向量,但是矩阵特征值不一定有0,所以退而求其次求最小)
全最小二乘的物理意义如下图,就是使所有数据点在直线的垂直方向上的投影最小。
鲁棒估计
最小二乘容易受到极端数据点的影响。
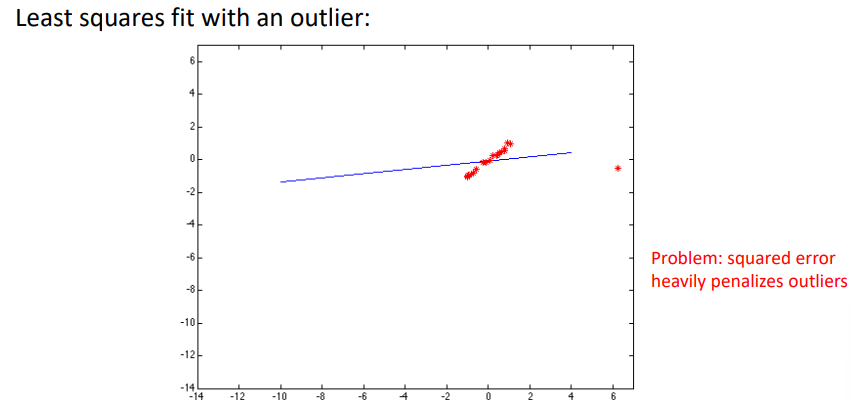
通过变换损失函数,当数据点距离直线越远时,损失会稳定到一个常数,从而减轻极端数据点的影响。$\sigma$是超参数,可以调整拟合对于外点的敏感性,具体见下图。
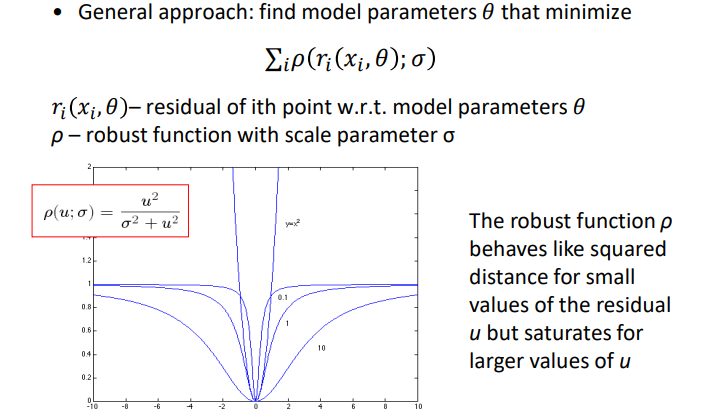
鲁棒最小二乘因为距离不是线性操作,所以最优参数需要通过迭代得到。为了加速迭代,可以使用最小二乘用于初始化。

评论