摘要
滤波作为计算机视觉中常见的一种操作,一般用于降噪、边缘提取等操作。滤波一般通过卷积操作完成,根据需要可以定制卷积核,实现均值/高斯/中值滤波。
卷积操作
卷积操作的示意图如下,给定卷积核g和图像f,卷积后的图像表示为
$$
(f*g)[m,n] = \sum_{k,l}f[m-k,n-l]g[k,l]
$$
根据上述公式中的负号,卷积核实际使用时,是将核上下左右翻转后再作用在图像f上。当然这个操作在实际编程时已经被淡化,只不过卷积定义要求了负号(翻转)

卷积具有两个特性:
- Linearity,即$filter(f_1+f_2) = filter(f_1)+filter(f_2)$
- Shift invariance,即$filter(shift(f)) = shift(filter(f))$
以上两个性质说明任何具有平移不变性的线性操作都可以用卷积操作表示。除此之外,卷积操作还满足交换律、结合律、分配律、数乘等操作。
卷积操作会改变图像的大小(联想deep learning中卷积层的padding),那么如何填充原始图像,保证结果图像和原图保持大小一致就是一个值得思考的问题。具体来说,可以通过填充0值、边缘复制、镜面反射等操作实现填充。

卷积核定制
图像平移
下图是最简单的卷积核,输出与原图保持一致。其中黑边是padding。
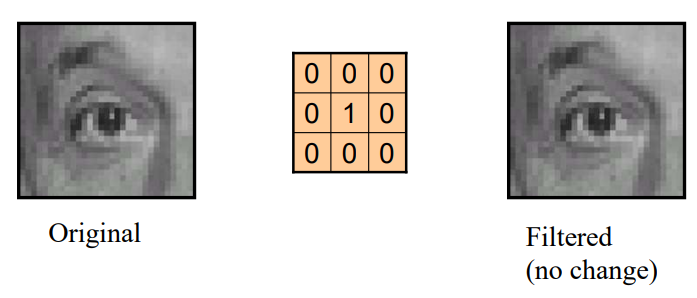
如果改变1的位置,那么会起到平移的作用,如下图。
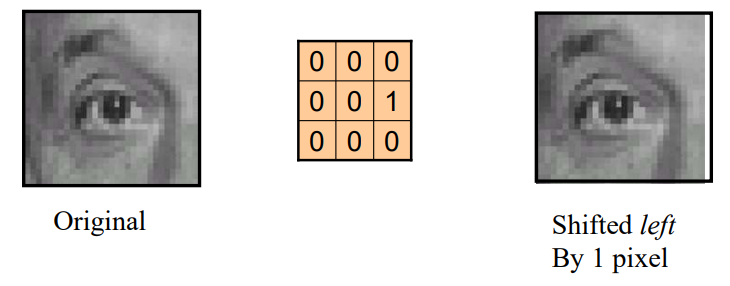
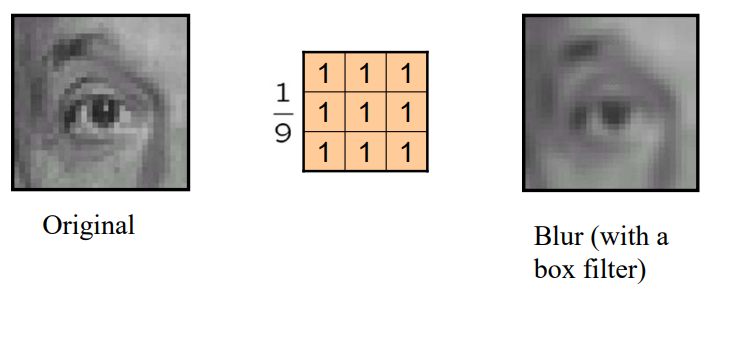
图像模糊(blur)
如果采用全1卷积核,那么中心点的像素值会是一个范围内像素值的平均,从而达到模糊的效果。1/9是为了保证整个卷积核的权重和为1,控制亮度。
如果使用如下两个卷积核相减,最后会得到锐化后的图像。因为原图减去模糊后的图像,会使边缘更加清晰。第一个卷积核中心值为2是为了保证卷积核相减后权值仍为1。
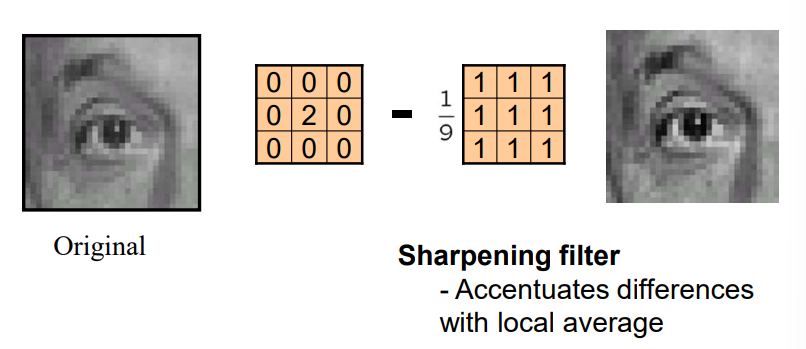
一个更具体的锐化例子如下。

高斯模糊
如果使用传统模糊卷积核,会出现振铃现象,即模糊后的图像会出现线条。

为了抵御这种现象,提出了高斯卷积。事实上,高斯卷积几乎在所有需要平滑的地方都会出现。高斯核中的权值计算如下,权重是和中心点距离有关的函数,距离中心点越远,对应的权值越小。当然最后结果需要归一化,保证高斯核权重和为1。
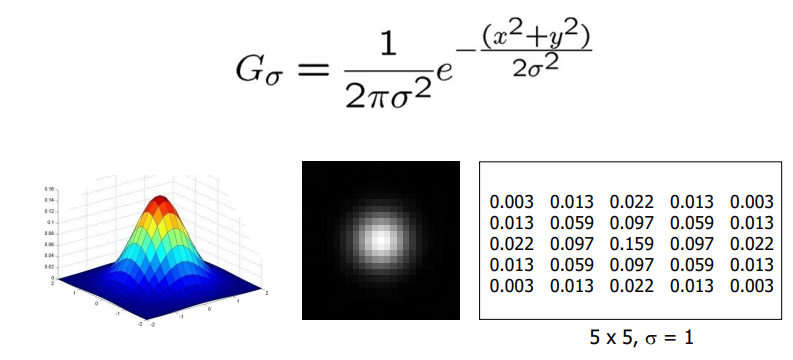
高斯核有两个参数,高斯核大小与标准差$\sigma$。一般两者大小关系采用$3\sigma$原则。
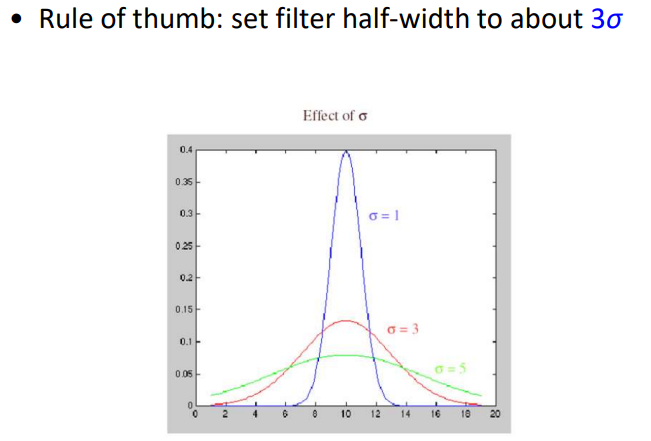
高斯卷积首先可以滤掉图像的高频部分,相当于低通滤波器。
其次卷积本身是另一种高斯,这句话理解为:两个高斯核的作用可以用一个更大的高斯核作用等效替代,例如执行两次标准差为$\sigma$的高斯模糊操作后,等效于执行一次标准差为$\sqrt 2 \sigma$的高斯模糊。
最后为了加速运算,可以使用两次一维高斯模糊操作来代替一次二维高斯模糊。这样时间复杂度就从$O(n^2m^2)->O(n^2m)$

噪声
噪声分为椒盐噪声、脉冲噪声、高斯噪声三种。

高斯噪声可以使用高斯模糊来去除,标准差越大,去噪越明显,不过图像也越模糊。

中值滤波
而对于椒盐噪声,高斯模糊效果就不是很好。因为高斯说白了还是平滑,但是椒盐噪声有很多突兀的像素点。这个时候使用中值滤波效果可能会更好。具体来说,该点像素值等于核中像素值序列的中间值。

锐化的形式化表示
锐化的形式化表示如下图,最后得到的卷积核是拉普拉斯高斯。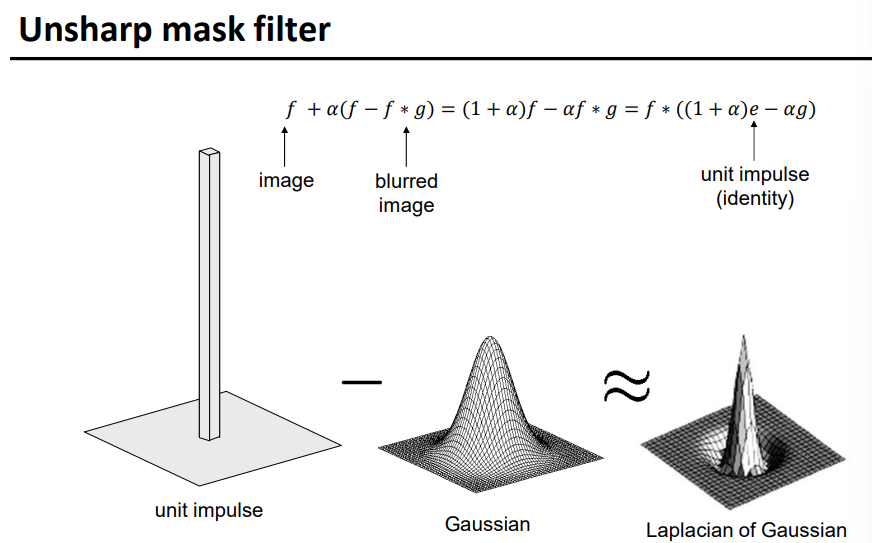

评论