摘要
这篇工作使用对抗性扰动来增强deepfake图像并绕过常见的deepfake检测器。使用FGSM和C&W L2 Attack在黑/白盒场景下进行测试。探测器在未扰动的deepfake上实现了超过95%的准确率,但在扰动的deepfake上的准确率低于27%。文章还探索了对deepfake检测器的两项改进:Lipschitz正则化以及深度图像先验
对抗扰动生成
FGSM这里就掠过不谈了,C&W $L_2$ Attack挺感兴趣的可以查看【学习笔记】对抗攻击:基于优化的CW攻击方法 - 知乎 (zhihu.com)
具体来说,论文使用的CW攻击设置如下。
首先是目标函数$f(x)$,选择
$$
f(\mathbf{x}^{\prime})=\operatorname*{max}(\operatorname*{max}_{i\neq y}\{\mathbf{Z}(\mathbf{x}^{\prime})_{y}-\mathbf{Z}(\mathbf{x}^{\prime})_{i}\},-\kappa).
$$
其中$Z(x)_y$指模型将x识别为真实类别y的概率(softmax前),$Z(x)_i$则是识别成目标类别i的概率。$\kappa$则是目标类别概率大于真实类别概率的阈值。
同时为了更好优化图像x,采用变量转换。原先是对x进行优化,现在转而优化$\omega$,而新图像$x'$表示为
$$
{\bf x}^{\prime}=\frac{1}{2}(\operatorname{tanh}(\omega)+1)
$$
优化$\omega$的方法如下
$$
\omega^{*}=\arg_{\operatorname*{min}}\{||{\bf x}^{\prime}-{\bf x}||_{2}^{2}+c\,f({\bf x}^{\prime})\}
$$
最终对抗样本则可以表示为
$$
{\bf x}_{adv}=\frac{1}{2}(\operatorname{tanh}(\omega ^*)+1)
$$
攻击效果如下图。
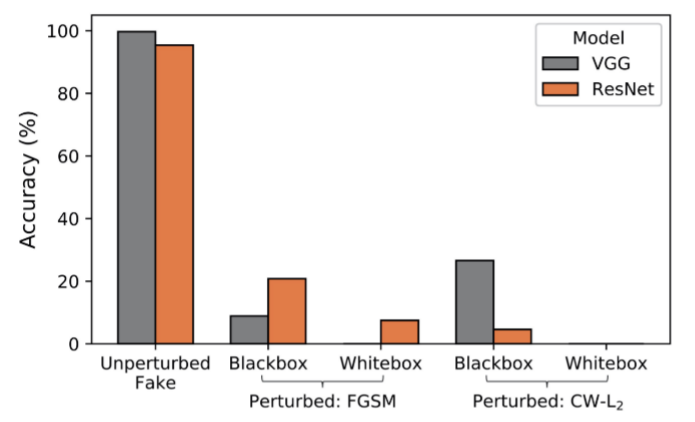
Lipschitz正则化
Lipschitz正则化主要是约束了检测器相对于输入的梯度。具体做法是在损失函数后多加一项
$$
J_{a u g}({\bf x},{\bf y},\theta)=J({\bf x},{\bf y},\theta)+\frac{\lambda}{C N}\sum_{i=1}^{C}||\nabla_{x}Z({\bf x})_i||^{2}.
$$
其中C是目标类别的总数,N是输入向量的维度,$\lambda$控制正则化的强度。结果如下图,虽然准确率有一定提升,但是提升不大。
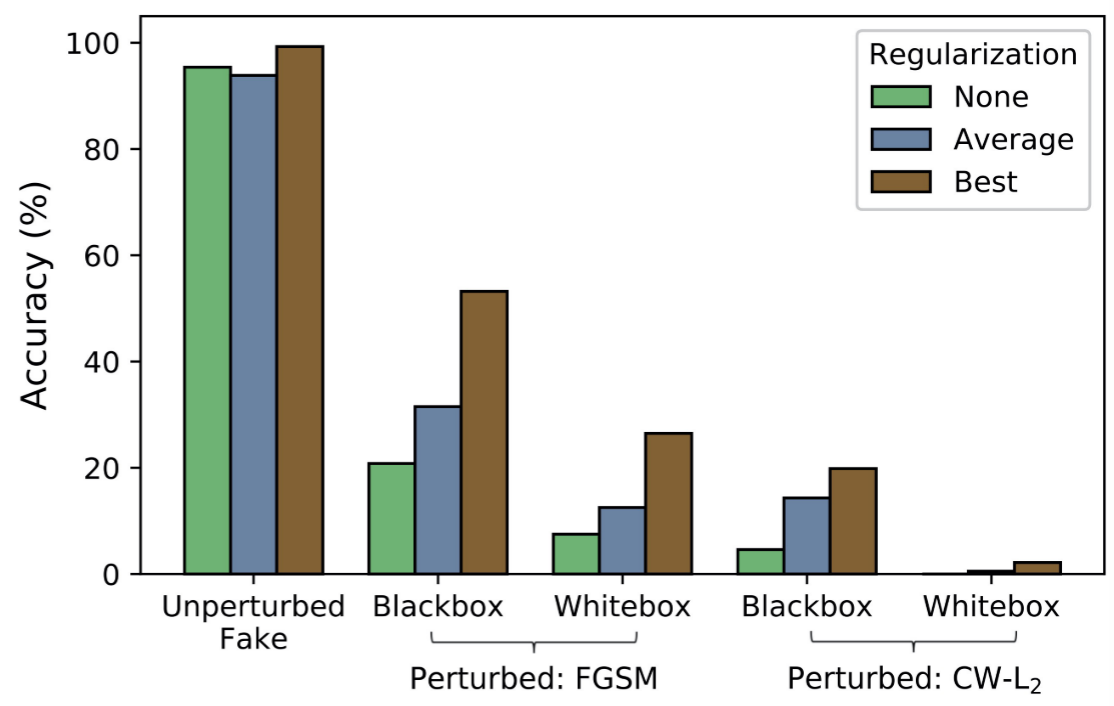
深度图像先验
深度图像先验,简单来说就是在输入之前训练一个CNN网络,这个网络负责输入图像的重建,将重建后的图像输入deepfake检测器中。这种重建有可能滤掉攻击者施加的对抗性扰动。
关于实验的具体设置,选择MSE作为重建损失,而关于generative CNN的具体网络结果没有提及。
实验效果如下图,可以看到随着训练轮数增加,分类器性能从好到逐渐变差。性能变差的主要原因在于CNN非常容易过拟合,训练到后期DIP图像重建发生过拟合从而影响分类器。观察以下四幅图片,发现在轮数为6500左右时分类器可以达到不错的性能。
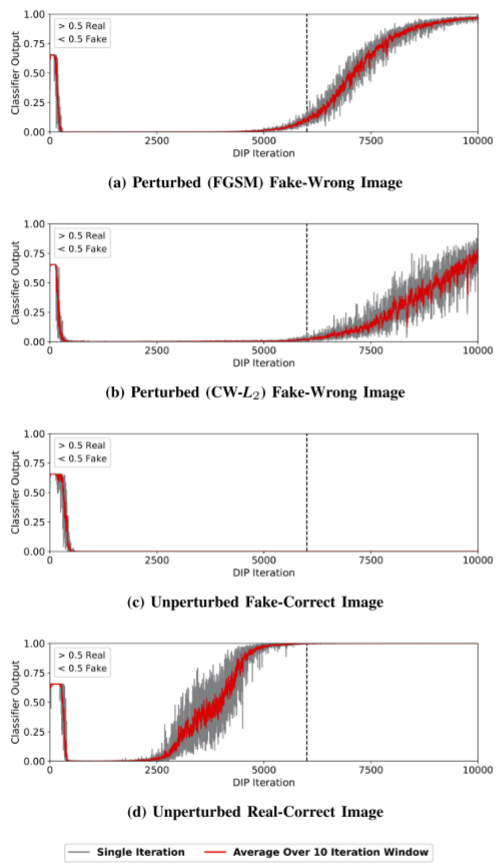
总结
这篇攻击主要探讨了deepfake检测器的防御方式,第一种是通过Lipschitz正则化限制模型关于输入的梯度变化;第二种基于图像重建来消除扰动。但是两种方式都具有局限性,例如Lipschitz正则化对于对抗样本的鲁棒性不足(性能提升不够明显),而图像重建对于训练轮数有较大限制。

评论