Evading DeepFake Detectors via Adversarial Statistical Consistency

深度学习 · 2023-05-15 · 618 人浏览
Evading DeepFake Detectors via Adversarial Statistical Consistency

摘要

论文地址： [2304.11670] Evading DeepFake Detectors via Adversarial Statistical Consistency (arxiv.org)](https://arxiv.org/abs/2304.11670)

本文主要提出了一种针对DeepFake检测器的统计一致性攻击(StatAttack)：选择DeepFake检测器的一些统计敏感性特征(natural degradations，例如图片的曝光、模糊以及噪声)，然后使用对抗性的方法将这些特征加入到Fake图片中，减小真图和假图之间的特征分布差异，从而欺骗检测器。

对抗训练中，因为注意到自然图像和DeepFake图像中的统计差异和两种图像之间的分布偏移成正相关，所以使用分布偏移感知损失(MMD,最大均值差异)来作为训练的损失函数。

最后文章还提出了一个攻击效果更好的MStatAttack，实际上就是在StatAttack基础上给各个增加的统计特征赋予权重(动态调整)，并多次迭代。

实验方面，文章在四个基于空间的检测器和两个基于频率的检测器分别测试了白盒、黑盒攻击的效果。

攻击原理

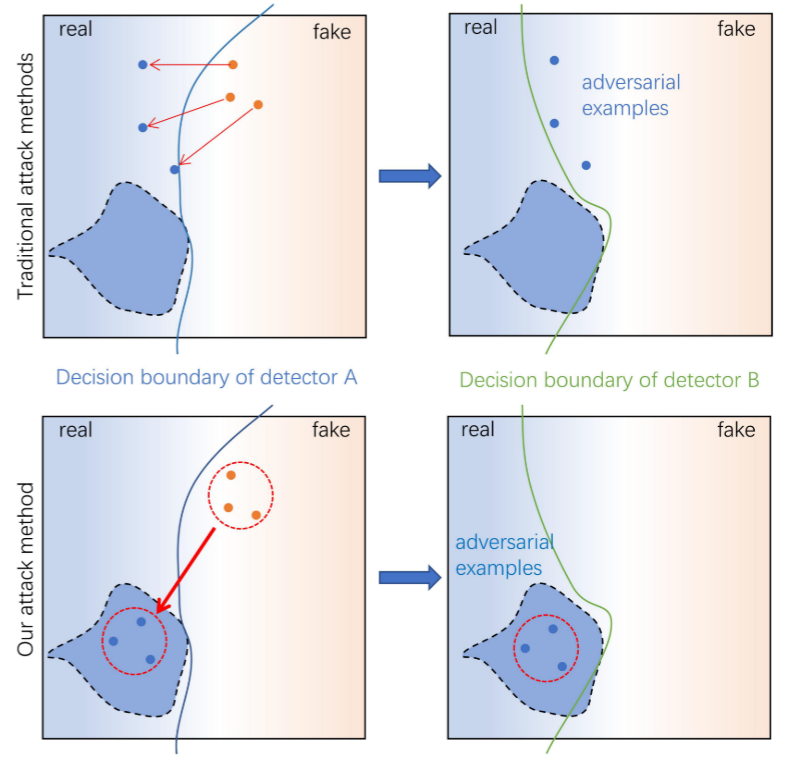
下图两列分别展示了DeepFake检测器A、B的决策边界，对于不同的检测器，由于网络结构、训练方式的不同，决策边界往往不同。因而限制住了对抗样本的迁移性，即攻击特定检测器生成的对抗样本大概率无法攻击其他检测器。

本文希望找到不同检测器之间的一块公共的嵌入区域，如果对抗样本落入这块区域，那么它对于这些检测器都具有欺骗性。下图第二行形象地展示了这个过程。

image-20230514103641073

统计差异

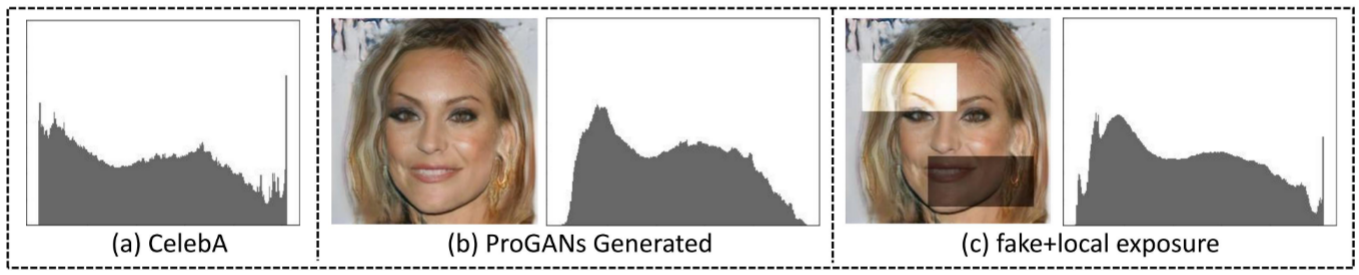
根据一些前人的工作得知：自然图像和GAN生成图像在频域和空间域上都存在差异。例如McCloskey表明两者存在亮度统计差异，GAN只能生成有限光强的图像，无法生成饱和或曝光不足的区域。Durall表明两者存在频率信息的统计差异，GAN会在图片上留下规律的高频痕迹(high-frequency artifacts)。

作者认为通过降低刚刚提到的自然图片与DeepFake图片之间频域/空间域差异(他称这个过程为自然退化，natural degradation),可以让DeepFake在检测器眼里更加真实。

这也意味着攻击原理中提到的公共区域是由这些统计特征指示的，换句话说作者认为不同检测器都能学习到自然图像和Fake图像之间的这些统计差异

自然退化

作者提出了三个方向降低上文提到的统计差异。

  • 改变曝光：通过调整图像局部区域中的亮度值，改变DeepFake的亮度分布，模拟饱和或曝光不足的区域，从而使亮度分布与自然图像分布相似。

    image-20230514105802382

  • 添加模糊：通过低通滤波器去除DeepFake中的高频分量，减少频域中的统计差异。

    image-20230514105805737

  • 添加噪声：通过添加随机噪声，去除图像频谱图中的regular artifacts。

    image-20230514105808068

这三种扰动都是通过对抗的方式生成的。每种方式都有可学习的参数，然后使用MMD Loss去优化。

我的理解是一种物理模拟，作者先假设检测器通过这种统计差异区分真假，也就意味着它学习到自然样本这些特征的分布(真实分布)，通过增加可学习的物理变换，并利用GAN去优化参数，从而使扰动后的Deepfake在这些特征上的分布更逼近真实分布。

改变曝光

改变曝光采用的是Gao的adversarial exposure generation model，模型包括两部分，产生曝光的多项式模型和保持曝光自然的平滑公式。
$$
P_e(X^{fake})=\log^{-1}(\tilde X^{fake} + \tilde E)
$$
其中$E$是曝光生成模型，$X^{fake}$是DeepFake图像，$\tilde ·$是对数操作。个人理解对数操作也实现保持曝光自然的平滑。

在$E$中有两个可学习参数$\alpha,φ$,用于优化曝光的生成。这里作者说为了让曝光更加自然，可以在损失函数加入下列平滑方程来约束参数值。(类似$L_2$正则)
$$
S(\alpha,φ) = -\lambda_a||a||_2^2 - \lambda_φ||\nabla φ||_2^2
$$
其中$\lambda_a,\lambda_φ$是超参数，用于调节曝光强度与平滑性之间的平衡。

添加高斯模糊

通过给图片添加高斯模糊，从而减少DeepFake中的高频分量。与普通高斯模糊不同，这里将高斯核设计成可学习的参数。这样允许在图像在不同位置自适应添加扰动。具体来说，首先生成一副和原图大小一致的标准偏差图$\sigma$ ,$\sigma$越大图片越模糊。通过$\sigma$也可以反推高斯核的值。例如第i个像素对应的高斯核为
$$
{\bf H}_{i}(u,v)=\frac{1}{2\pi\left(\sigma_{x_{i},y_{i}}\right)^{2}}e x p\left(-\frac{u^{2}+v^{2}}{2\pi\left(\sigma_{x_{i},y_{i}}\right)^{2}}\right)
$$
其中u和v表示高斯核内的点与高斯核中心像素$(x_i,y_i)$的相对坐标。随后可以计算高斯模糊后的图像
$$
P_{b}(\mathbf{X}^{\mathrm{fake}})=\sum_{i\in{\cal{N}}(i)}g(\mathbf{X}_{i}^{\mathrm{fake}},k)*\mathbf{H}_{i}
$$
其中$\cal{N}(i)$表示$X^{fake}$中的所有像素，$g(X^{fake},k)$表示在图中第i个像素附近，包括于半径为k的高斯核内的范围。

优化参数时，通过loss函数的反向传播更新标准偏差图$\sigma$，那么每个像素对应的高斯核也被更新。最后通过优化后的高斯核对Deepfake施加像素级别的高斯模糊。

添加噪声

这部分和以往工作一致，往DeepFake中添加随机噪声$N_a$。通过最小化Loss对$N_a$进行更新。
$$
P_{n}(\mathbf{X}^{\mathrm{fake}})=\mathbf{X}^{\mathrm{fake}}+\mathbf{N}_{a}
$$

StatAttack

StatAttack应用上述的三种方法，得到最终的扰动图像
$$
P_{\theta}(\mathbf{X}^{\mathrm{fake}})=P_{n}(P_{b}(P_{e}(\mathbf{X}^{\mathrm{fake}})))
$$
其中$P_{\theta}(X^{fake})$包括以下优化参数$\{\alpha,φ,\sigma,N_a\}$

损失函数本文使用的是最大均值差异(MMD)，这是一个统计学的概念。具体是通过随机变量的矩来确定两个数据分布的距离。具体可以看这篇统计知识（一）MMD Maximum Mean Discrepancy 最大均值差异 - 知乎 (zhihu.com)
$$
M M D[F,p,q]=\operatorname*{sup}_{||f||_{H}\leq1}E_{p}[f(x)]-E_{q}[f(y)]
$$
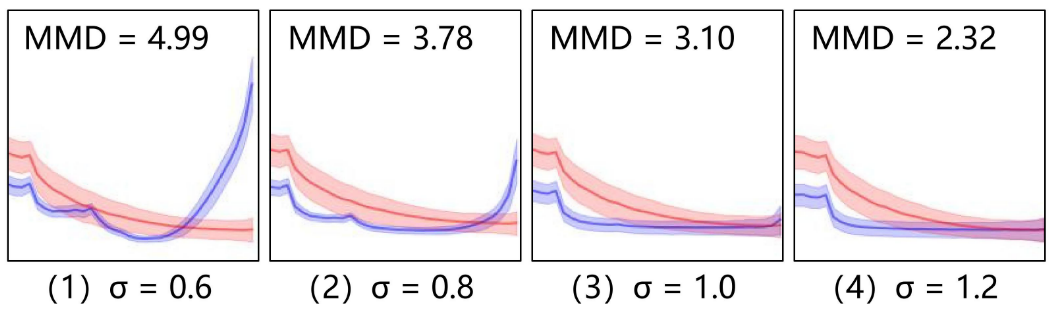
文章解释了为什么使用MMD作为损失函数。之前提到过GAN生成的图像在高频分量的能量较大，通过高斯模糊可以滤去高频信息。而随着高频信息的过滤(参数体现为$\sigma$的增大)，统计量MMD也呈下降的趋势。并且MMD是端到端可微的，所以作者认为可以通过MMD指导损失。

image-20230514131946798

综上，优化目标可以表示成
$$
\begin{array}{c}{{a r g\,\mathrm{min}\mathrm{J}_{M M D}\left(P_{\theta}\,\left(\chi^{\mathrm{{fake}}}\right)\,,\,\chi^{\mathrm{{real}}}\right)}}\end{array}+S(\alpha,φ),||N_a||_p \leq \epsilon
$$

这里限定了$N_a$的$L_p$范数，同时也提到了使用约束项强制$N_a$具有稀疏性，所以这里应该p=1

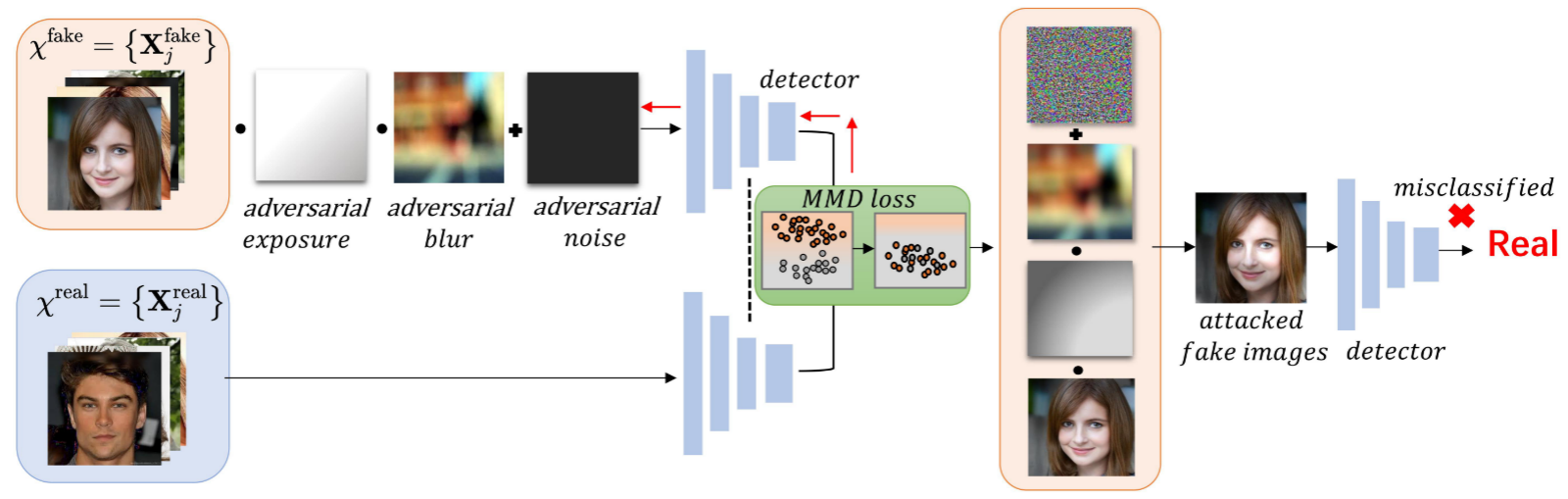
StatAttack可以总结为下图，首先对DeepFake施加之前提到的三种退化，接下来在检测器的全局池化层上收集自然图像和DeepFake的特征分布，并计算它们的MMD Loss，通过反向传播更新自然退化的参数$\{\alpha,φ,\sigma,N_a\}$，最后将更参数后的结果应用在DeepFake，从而欺骗DeepFake检测器。

image-20230514133012992

Multi-layer StatAttack

MStatAttack相比于StatAttack，主要多了以下两点改进：

  • 单层退化拓展到多层退化
  • 使用自适应权重调整每种退化的占比

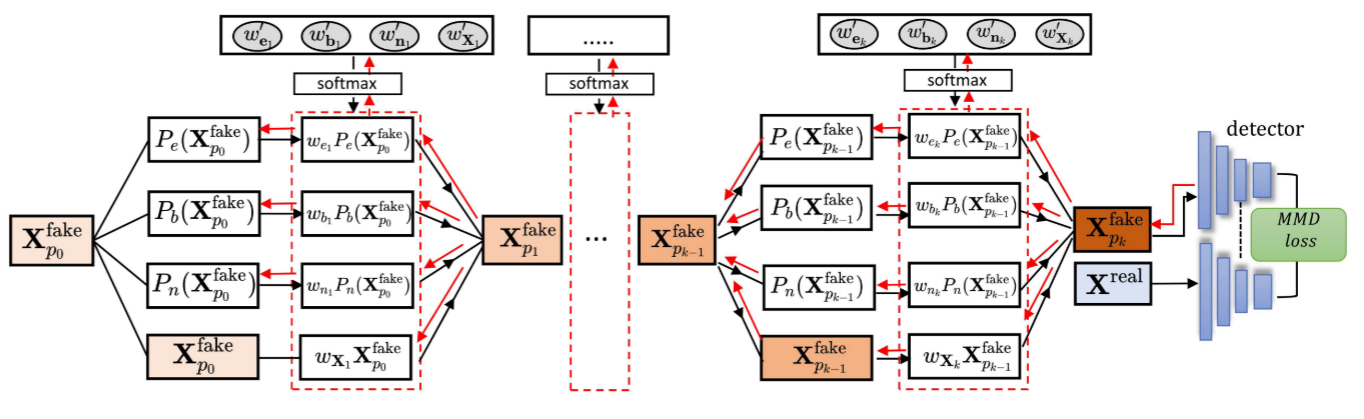
image-20230514133605483

单层扰动可以表示为
$$
\mathbf{X}_{p_{k}}^{\mathrm{fake}}=w_{e_{k}}P_{e}(\mathbf{X}_{p_{k-1}}^{\mathrm{fake}})+w_{b_{k}}P_{b}(\mathbf{X}_{p_{k-1}}^{\mathrm{fake}})+w_{n_{k}}P_{k}({\bf X}_{p_{n-1}}^{\mathrm{fake}})+w_{{X}_{k}}{\bf X}_{p_{k-1}}^{\mathrm{fake}}
$$
这里四个权重值需要做softmax，保证权重总和为1，防止图像混合过程中给的强度溢出。

实验结果

实验设置

  • 数据集：总共收集了四种数据集，包括面部合成、属性替换、身份交换三种类型

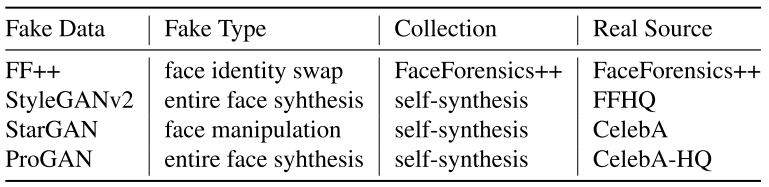
    image-20230514145332584

  • 受害者模型：四种基于空间的检测器(ResNet50,EfficentNet-b4,DenseNet,MobileNet)，两种基于频率的检测器(DCTA,DFTA)

    image-20230514145631383

  • 评估手段：攻击成功率(ASR)与图像质量度量(BRISQUE)

  • Baseline Attack：PGD 与 FGSM，以及两种SOTA可迁移攻击MIFGSM与VMIFGSM

攻击效果

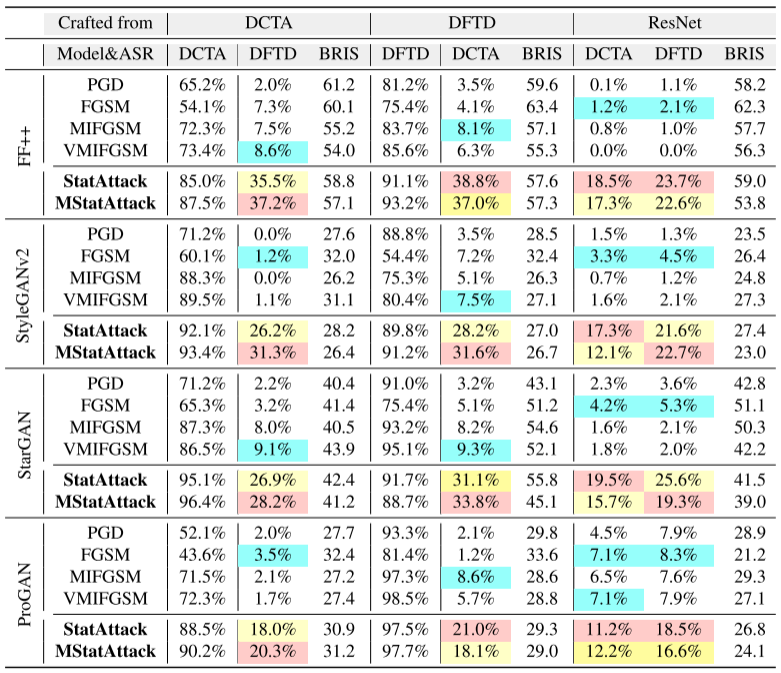
1.攻击基于空间的四个检测器

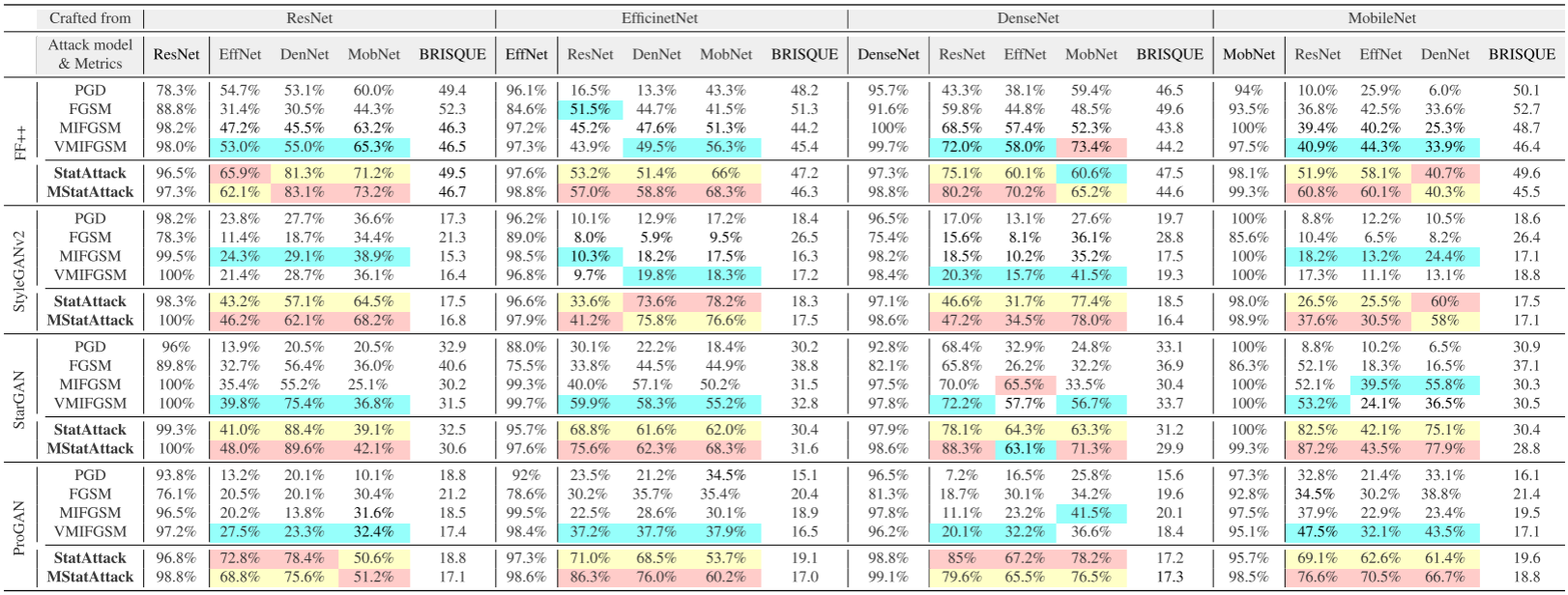
image-20230514150057940

其中红、黄、蓝颜色标识攻击成功率的前三名。

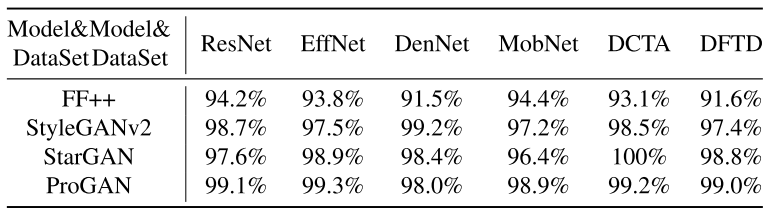
2.攻击基于频率的四个检测器

image-20230514150307995

3.消融实验

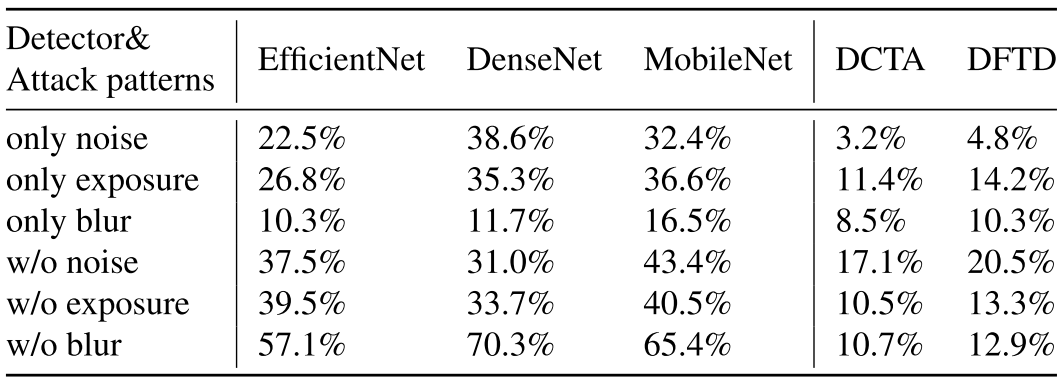
image-20230514150410392

上表表明：对于基于空间的检测器，噪声和曝光两种操作对其影响较大；对于基于频域的检测器，主要受曝光和高斯模糊的影响。

总结

这篇工作以自然图像与DeepFake图像之间存在的统计差异为出发点，通过添加对抗性扰动弥补这种差异，达到欺骗检测器的效果。

具体来说，文章选择了三种方式(添加曝光、模糊、噪声)弥补deepfake在空间域/频域的缺陷，每种方法都具有可学习的参数，参数由$MMD Loss$指导更新。$MMD Loss$可以感知并量化两张图片的统计差异(例如高频分量的多少)。基于以上思想，文章提出了StatAttack和MStatAttack，MStatAttack相比于StatAttack多了权重适应和多层退化。

最后文章在4个数据集上对6种检测器进行白盒/黑盒测试，同时横向对比了PGD/MIFGSM等其他攻击方式。通过消融实验也得出不同退化对于不同类型检测器的攻击效果。

deepfake adversarial attack
2023 - 2025 Axuanz的学习日记. All Rights Reserved.
Theme Jasmine by Kent Liao