摘要
基于WGAN提出了一个攻击黑盒分类器的自然对抗样本生成框架。这些自然对抗样本可以帮助解释黑盒模型的决策行为和评估的准确性。最后在图像分类、文本蕴含和机器翻译上进行了测试。
网络训练
相比于GAN/WGAN,NaturalGAN多了一个部件逆变器(Inverter$I$).逆变器的作用是将原始样本x映射回低维的稠密向量空间.
这样做的原因在于:GAN生成器的输入是随机的低维高斯噪声z(比如dim=100),通过生成器G映射到高维空间,这个分布在高维空间是低维流形,也就是所谓的“撑不满”整个高维空间(这个在之前在WGAN中提到过).换句话说生成的对抗样本$x'$的分布其实很大程度上取决于低维噪声的分布.而GAN直接拿随机噪声作为G的输入,而忽略了真实样本x的分布$p_r$,尽管通过设置损失函数(JS散度或EM距离)可以拉近$p_r$和$p_g$,但是缺少了原始样本x的特征信息,会导致最终生成的对抗样本不够自然.
在AdvGAN中,是通过输入样本x或样本x的特征图来解决上述不足
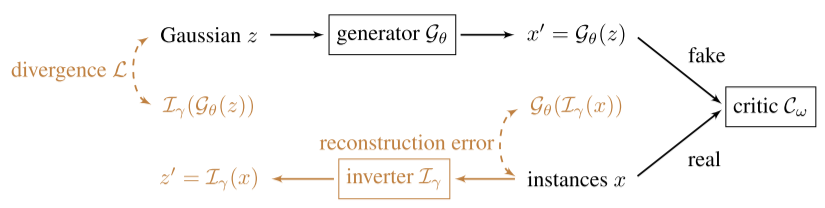
回到NatualGAN,训练共分两个步骤.首先是按照WGAN的策略,训练好生成器G和判别器C.这里G的输入暂时还是随机的高斯噪声.最大最小博弈函数为(EM距离)
$$
\operatorname*{min}_{\theta}\operatorname*{max}_{\omega}\mathbb{E}_{x\rightarrow p_{x(x)}}\left[C_{\omega}(x)\right]-\mathbb{E}_{z\sim p_{z(z)}}\left[C_{\omega}(G_{\theta}(z))\right]
$$
训练第二步即上图中的黄色部分,固定判别器C,训练逆变器$I$和生成器G.$I$的输入是原始样本$x$,输出是和噪声$z$在同一维度空间的$z'$.对于判别器$I$,我们想得到的效果是:
- 输入原始样本$x$产生的输出$z'$,将其输入到$G$中生成的新样本$x'$,应该和$x$足够接近(保证自然).这一部分可以称为重建误差(reconstruction error).
- 对于某一噪声$z$经$G$生成的样本$x'$,将其输入到$I$中得到的输出$z'$.$z$和$z'$的分布应该足够接近.这一部分是训练逆变器$I$的映射能力.
综上两点可以得到$I$(也包括$G$)的损失函数.
$$
\operatorname*{min}_{\gamma}\mathbb{E}_{x\sim p_{x}(x)}\|G_{\theta}(I_{\gamma}(x))-x\|+\lambda\cdot\mathbb{E}_{z\sim p_{z}(z)}[{\mathcal{L}}(z,I_{\gamma}(G_{\theta}(z)))]
$$
当距离$\mathcal{L}$使用$L_2 distance$时,$\lambda$=0.1(for images)
当距离$\mathcal{L}$使用$Jensen-Shannon distance$时,$\lambda$=1(for text data)
对抗样本生成
$G,C,I$都训练结束后,可以定义对抗样本为
$$
x^{*}=G_{\theta}(z^{*}){\mathrm{~where~}}z^{*}=\arg\operatorname*{min}_{\tilde{z}}\parallel\tilde{z}-\mathbb{Z}_{\gamma}(x)\parallel\operatorname{s.t.}f(G_{\theta}({\tilde{z}}))\neq f(x)
$$
即首先将原始样本x输入到逆变器$I$中,得到低维向量$z'$,随后对$z'$产生一定扰动生成$\tilde z$.找到扰动最小的$z$,使$f(G(\tilde z))\neq f(x) $.
扰动最小自然是为了保证对抗样本足够自然

关于$\tilde z$的搜索,论文给了两种算法.一种是逐渐增加扰动的暴搜算法,另一个是基于二分的粗粒度到细粒度的搜索算法.具体看图~


算法二先通过二分确定扰动范围(<$\delta r$),然后再爆搜.算法效率是算法一的四倍,效果可以持平算法一
生成结果
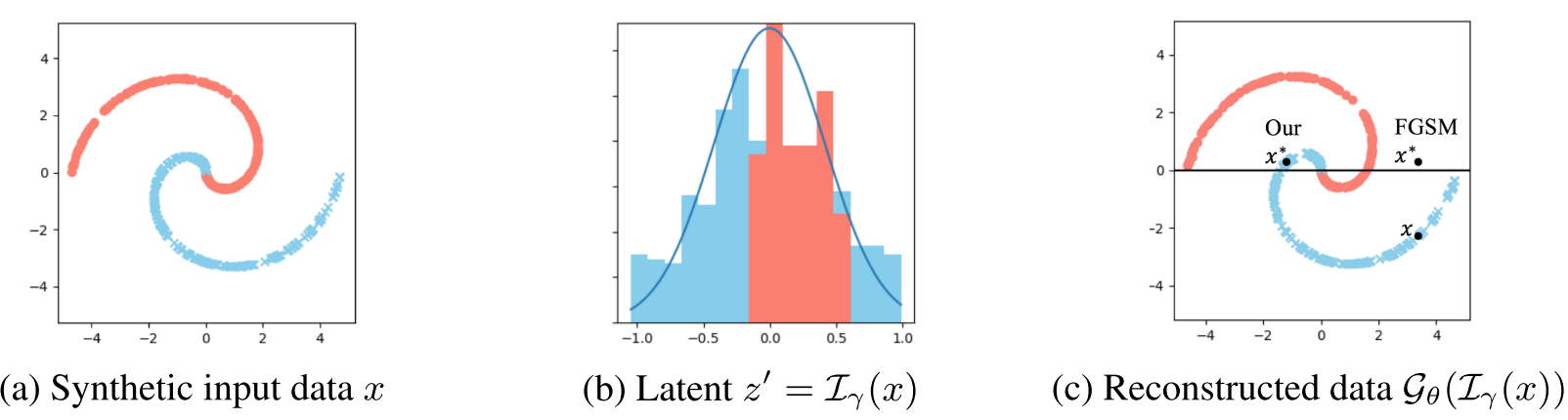
先看一对有意思的图,*图片(a)是数据x的分布情况,图(b)是逆变器的输出结果,可以看到$z'$基本满足正态分布,图(c)显示了二元分类器的决策边界以及NatualGAN生成的对抗样本$x^(Our)$的位置**.而通过FGSM生成的对抗样本可能在右侧.虽然两者都使辨别器犯错,但是$x^*(Our)$在蓝色样本的流形上,无疑会更加自然.
最后是在MNIST手写数字数据集上的对比测试.


评论