简介
论文地址 Generating Adversarial Examples with Adversarial Networks|IJCAI 2018
本篇论文基于GAN生成对抗样本。首先提出训练一个产生扰动的前馈网络(G)来生成不同的对抗样本,再通过一个判别网络(D)判别扰动图像的真实性。并在半白盒和黑盒两种场景下进行实验。由于条件GANs能够生成高质量的图像,他们使用了类似的范例(LSGAN)来生成对抗样本。
在以前的白盒攻击中,如FGSM和优化方法,对手需要有攻击的目标模型的架构和所有参数。然而,通过部署AdvGAN,一旦G得到训练,它可以立即为任何输入样本产生扰动,而不再需要访问模型本身。此攻击场景称之为半白盒。
网络主体
问题定义
假设$X \subseteq R^n$为特征空间,n为特征维度。设训练集中的一个样本($x_i,y_i$),其中$x \subseteq X$,并服从分布$\mathbf{x_{i}}\sim\mathbf{P}_{\mathrm{data}}$,且$y_i \in Y$.攻击的目标网络是一个分类器$\mathbf{f}:{\boldsymbol{X}}\rightarrow{\boldsymbol{Y}}$,将样本空间映射到分类集合的大小,$|Y|$即分类输出的数量.对于一个样本x,攻击者的目标是生成对抗样本$x_A$,使$f(x_A) \neq y$(非定向攻击),其中y是x对应的真实标签;或者实现$f(x_A) = t$(定向攻击),其中t是目标类别.除此之外,$x_A$也应该在$L_2$等其他度量上与原始样本x足够接近(隐蔽性).
AdvGAN框架与白盒攻击
下图展示了AdvGAN的总体架构,主要由生成器$G$、判别器$D$和目标神经网络$f$三部分组成。这里生成器$G$以初始实例$x$为输入,产生扰动$G(x)$。然后将$x+G(x)$发送给判别器$D$,用来区分生成的数据和原始实例$x$。首先执行白盒攻击,在本例中,目标模型是$f$。$f$以$x + G ( x )$为输入输出其损失$L_{adv}$,表示预测类别与目标类 $t$ (定向攻击)之间的距离,或预测值(除去真实类别外概率最大的那个类别的概率值)与真实类别的(非定向攻击)之间的距离。
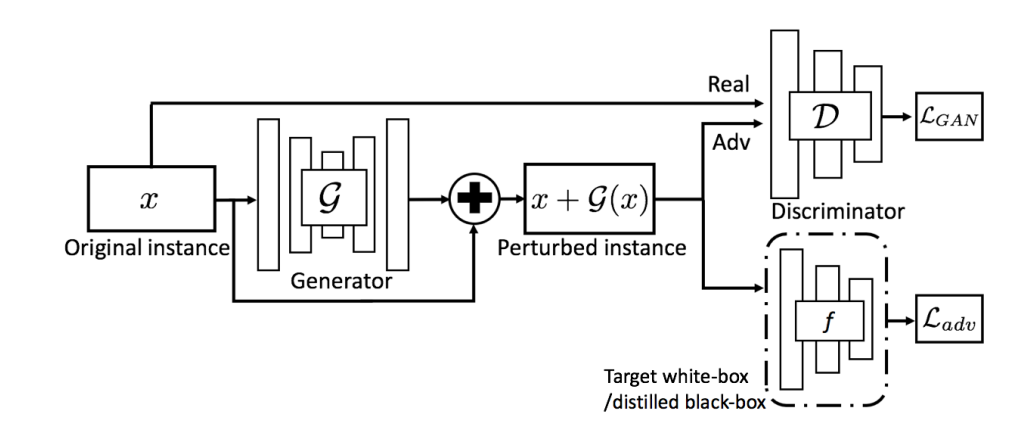
对于GAN那一部分,损失函数可以写成
$$
\left.{\mathcal{L}}_{\mathrm{GAN}}=\mathbb{E}_{x}\log D(\mathbf{x})+\mathbb{E}_{x}\log(1-{\mathcal{D}}(\mathbf{x}+{\mathcal{G}}(\mathbf{x}))\right)
$$
这部分和原始的GAN网络的损失函数基本一致,只不过原始公式第二项$D$的输入直接是$G(z)$,而不是原始图像加扰动值$x+G(x)$.因为GAN是用$G$生成图像,这里的$G$只是生成扰动.通过$L_{GAN}$,$G$和$D$将不断迭代,最终使$G$生成与原图差别不大(加上$x$后)的扰动$G(x)$.
对于需要攻击的目标模型,我们定义$f$的损失函数为
$$
{\mathcal{L}}_{\mathrm{adv}}^{\mathrm{f}}=\operatorname{E}_{\mathbf{x}}1_{\mathbf{f}}\left(\mathbf{x}+g(\mathbf{x}),\mathbf{t}\right)
$$
这里的$t$是目标类别,$l_f$是目标模型$f$的损失函数(比如交叉熵),通过$L_{adv}$,可以鼓励$x+G(x)$被目标模型$f$分类到错误的类别$t$中.当然这是定向攻击的写法,对于非定向攻击,将在代码部分讲解.
还有一项损失是Hinge Loss,用于限制扰动的大小,之前在机器学习常常用作正则项.(有时间可以单独写一章细说).
$$
{\mathcal{L}}_{\mathrm{hinge}}=\mathbb{E}_{\mathbf{x}}{\mathrm{max}}(0,||G(\mathbf{x})||_{\mathbf{x}}-\mathbf{c})
$$
这里的$c$是超参数,限定扰动$G(x)$的$L_2$范数在c之内.至此损失函数就结束了,总结为
$$
{\mathcal{L}}={\mathcal{L}}_{\mathrm{adv}}^{\mathrm{f}}+\alpha{\mathcal{L}}_{\mathrm{GAN}}+\beta{\mathcal{L}}_{\mathrm{huge}}
$$
这里的$\alpha,\beta$分别是$L_{GAN},L_{Hinge}$的权重.训练时和GAN一致,使用最大最小博弈迭代$G,D$.训练完成后,可以用$G$对输入的任何样本产生扰动,这个时候就不再需要对$f$进行查询了,所以是一种半白盒的攻击方式.
$$
argmin_Gmax_D{\mathcal{L}}
$$
黑盒攻击与动态蒸馏
对于黑盒攻击,我们假设攻击者事先不知道训练数据或模型本身。所以需要随机抽取与黑箱模型训练数据不相交的数据进行蒸馏。为了实现黑盒攻击,首先需要在黑盒模型b的输出基础上构建一个蒸馏网络$f$[Hinton et al., 2015]。一旦得到蒸馏网络$f$,就可以执行与白盒设置相同的攻击策略。这里,通过最小化以下期望使蒸馏模型与和黑盒模型足够接近.
$$
\arg\operatorname*{min}_{f}\mathbb{E}_{\mathbf{x}}\mathcal H(\mathbf{f}(\mathbf{x}),\mathbf{b}(\mathbf{x}))
$$
其中f(x)和b(x)分别表示蒸馏模型和黑盒模型对给定训练图像x的输出,$\mathcal H$表示常用的交叉熵损失。通过对所有训练图像的目标进行优化,可以得到一个非常接近黑盒模型$b$的模型$f$,然后对蒸馏网络进行攻击。
值得注意的是,不像训练判别器 $\mathcal D$那样(输入原始样本和扰动样本),这里只使用真实数据来训练蒸馏模型$f$,并使用所有类的数据来训练。(很好理解吧)
动态蒸馏
上述的蒸馏方法是一种静态蒸馏,即提前训练好蒸馏模型$f$,接下来的攻击都用它来代替黑盒模型$b$.这有个坏处是:我们不清楚黑盒和蒸馏模型对生成的对抗样本的判断情况(因为压根没训练过),也就无法保证对于对抗样本它们俩的表现一致.
动态蒸馏的方式是在训练生成器$D,G$过程中,联合训练蒸馏模型$f$.具体来说分为以下两个步骤.
- 对于固定的$f_{i-1}$,训练$G,D$
这里和白盒攻击的优化策略一致,对于固定的$f_{i-1}$,通过最大最小博弈更新$G,D$.
$$
G_{\mathrm{i}},\mathrm{D}_{\mathrm{i}}\,=\,\mathrm{arg\,min}_{\mathcal{G}}\,\mathrm{max}_{\mathcal{D}}\,\mathcal{L}_{\mathrm{adv}}^{\mathrm{f}_{\mathrm{i}}\,-\,1}\,+\alpha\mathcal{L}_{\mathrm{GAN}}\,+\,\beta\mathcal{L}_{\mathrm{hinge}}
$$
- 对于固定的生成器$G$,更新$f_i$
更新$f_{i}$的损失函数有两项,第一项保证对于原始样本x,$f$的表现和黑盒模型$b$一致.第二项保证了对于对抗样本$x+G(x)$的相同表现.
$$
\mathrm{f}_{i}=\arg\operatorname*{min}\mathbb{E}_{x}\,H(\mathbf{f}(\mathbf{x}),\mathrm{b}(\mathbf{x}))+\mathbb{E}_{x}\,H(\mathbf{f}(\mathbf{x}+{\mathcal{G}}_{\mathrm{i}}(\mathbf{x})),\mathrm{b}(\mathbf{x}+{\mathcal{G}}_{\mathrm{i}}(\mathbf{x})))
$$
作者在这里测试了一下静态蒸馏与动态蒸馏的性能,突出动态蒸馏的优越性.
第一行是几个模型对于原始样本的准确率,第二行是半白盒攻击的攻击成功率,第三行和第四行分别是动态蒸馏和静态蒸馏下的攻击成功率.可以看到效果还是很明显的.
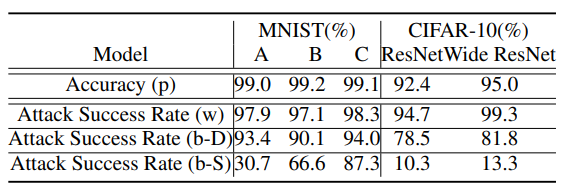
实验结果
作者首先评估AdvGAN在MNIST和CIFAR-10上的半白盒和黑盒攻击方式,还对ImageNetdataset进行了半白盒攻击。随后对于不同防御手段下测试了AdvGAN的攻击成功率,并表明与其他现有攻击策略相比,AdvGAN方法可以实现更高的攻击成功率。(在基于$L_\infty$约束的MNIST的0.3阈值和CIFAR-10的8阈值上进行公平比较)。Adv-GAN具有优于其他白盒和黑盒攻击的几个优点。例如,关于计算效率,AdvGAN执行速度比其他人快得多,甚至包括有效的FGSM,尽管AdvGAN需要额外的训练时间来训练生成器。除了基于可转移性的攻击,所有对比的模型都可以进行定向攻击,(通过集合策略可以帮助改进Trans Attack)。此外,FGSM和优化方法只能执行白盒攻击,而AdvGAN能够在半白盒设置中进行攻击。
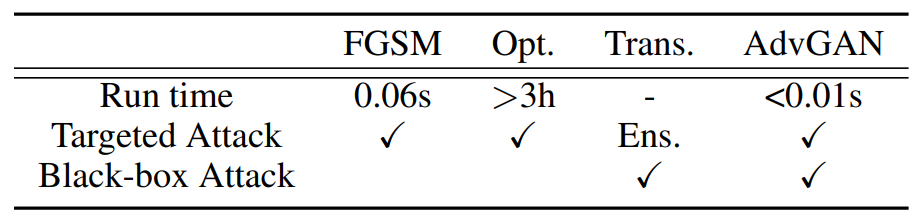
代码部分
参考这里的半白盒攻击实现mathcbc/advGAN_pytorch,使用MNIST数据集
和之前的GAN源码主要有以下几点不同:
- 训练AdvGAN前还需要训练所攻击的目标模型
- 生成器$G$的实现,这里采用了encoder-decoder架构,并且输出的是扰动
- 损失函数,多了Hinge Loss和$L_{adv}$.
目标模型
MNIST数据集是识别手写数字的(0~9),输入的图片维度是[1,28,28].训练参数采用Adam,lr=0.001,用了学习率衰减,详见代码.
# Target Model definition
class MNIST_target_net(nn.Module):
def __init__(self):
super(MNIST_target_net, self).__init__()
self.conv1 = nn.Conv2d(1, 32, kernel_size=3)
self.conv2 = nn.Conv2d(32, 32, kernel_size=3)
self.conv3 = nn.Conv2d(32, 64, kernel_size=3)
self.conv4 = nn.Conv2d(64, 64, kernel_size=3)
self.fc1 = nn.Linear(64*4*4, 200)
self.fc2 = nn.Linear(200, 200)
self.logits = nn.Linear(200, 10)
def forward(self, x):
x = F.relu(self.conv1(x))
x = F.relu(self.conv2(x))
x = F.max_pool2d(x, 2)
x = F.relu(self.conv3(x))
x = F.relu(self.conv4(x))
x = F.max_pool2d(x, 2)
x = x.view(-1, 64*4*4)
x = F.relu(self.fc1(x))
x = F.dropout(x, 0.5)
x = F.relu(self.fc2(x))
x = self.logits(x)
return x
# train
target_model = MNIST_target_net().to(device)
target_model.train()
opt_model = torch.optim.Adam(target_model.parameters(), lr=0.001)
epochs = 40
for epoch in range(epochs):
loss_epoch = 0
if epoch == 20:
opt_model = torch.optim.Adam(target_model.parameters(), lr=0.0001)
for i, data in enumerate(train_dataloader, 0):
train_imgs, train_labels = data
train_imgs, train_labels = train_imgs.to(device), train_labels.to(device)
logits_model = target_model(train_imgs)
loss_model = F.cross_entropy(logits_model, train_labels)
loss_epoch += loss_model
opt_model.zero_grad()
loss_model.backward()
opt_model.step()生成模型$G$
这里的G与GAN中的G不同.GAN中的G以噪声z为输入,直接通过转置卷积生成图像.而这里的G输入是原始图像,生成扰动.所以采用encoder-decoder结构,首先通过卷积构成的encoder提取输入样本的信息,再通过转置卷积decoder输出生成的扰动.
值得注意的是,这里的decoder中使用了InstanceNorm2d而不是BatchNorm.两者的区别是BatchNorm是针对一批样本中的相同特征做归一化,而InstanceNorm是在单个样本内做归一化.(LayerNorm也是在样本内做归一化)
在encoder与decoder之间还使用了残差块组成的bottle_neck.
class Generator(nn.Module):
def __init__(self,
gen_input_nc,
image_nc,
):
super(Generator, self).__init__()
encoder_lis = [
# MNIST:1*28*28
nn.Conv2d(gen_input_nc, 8, kernel_size=3, stride=1, padding=0, bias=True),
nn.InstanceNorm2d(8),
nn.ReLU(),
# 8*26*26
nn.Conv2d(8, 16, kernel_size=3, stride=2, padding=0, bias=True),
nn.InstanceNorm2d(16),
nn.ReLU(),
# 16*12*12
nn.Conv2d(16, 32, kernel_size=3, stride=2, padding=0, bias=True),
nn.InstanceNorm2d(32),
nn.ReLU(),
# 32*5*5
]
bottle_neck_lis = [ResnetBlock(32),
ResnetBlock(32),
ResnetBlock(32),
ResnetBlock(32),]
decoder_lis = [
nn.ConvTranspose2d(32, 16, kernel_size=3, stride=2, padding=0, bias=False),
nn.InstanceNorm2d(16),
nn.ReLU(),
# state size. 16 x 11 x 11
nn.ConvTranspose2d(16, 8, kernel_size=3, stride=2, padding=0, bias=False),
nn.InstanceNorm2d(8),
nn.ReLU(),
# state size. 8 x 23 x 23
nn.ConvTranspose2d(8, image_nc, kernel_size=6, stride=1, padding=0, bias=False),
nn.Tanh()
# state size. image_nc x 28 x 28
]
self.encoder = nn.Sequential(*encoder_lis)
self.bottle_neck = nn.Sequential(*bottle_neck_lis)
self.decoder = nn.Sequential(*decoder_lis)
def forward(self, x):
x = self.encoder(x)
x = self.bottle_neck(x)
x = self.decoder(x)
return xAdvGAN损失函数
损失函数分为三部分,代码实现里$\sigma$是10,$\alpha$是1,$\beta$是1.跟论文里不太一样.
$$
{\mathcal{L}}=\sigma{\mathcal{L}}_{\mathrm{adv}}^{\mathrm{f}}+\alpha{\mathcal{L}}_{\mathrm{GAN}}+\beta{\mathcal{L}}_{\mathrm{huge}}
$$
- 对于第二部分$L_{GAN}$,与原始GAN中的实现类似.区别在于损失计算不再使用当时的BCELoss,改用MSELoss.除此之外还是用了clipping trick限制了扰动的范围.(使$L_\infty$限制在一定范围内,上述提到MNIST数据集给的阈值是0.3).关键代码如下
# optimize D
perturbation = self.netG(x)
# add a clipping trick
adv_images = torch.clamp(perturbation, -0.3, 0.3) + x
adv_images = torch.clamp(adv_images, self.box_min, self.box_max)
self.optimizer_D.zero_grad()
pred_real = self.netDisc(x)
loss_D_real = F.mse_loss(pred_real, torch.ones_like(pred_real, device=self.device)) #use MSELoss instead of BCELoss
loss_D_real.backward()
pred_fake = self.netDisc(adv_images.detach())
loss_D_fake = F.mse_loss(pred_fake, torch.zeros_like(pred_fake, device=self.device)) # MSE
loss_D_fake.backward()
loss_D_GAN = loss_D_fake + loss_D_real
self.optimizer_D.step()
# optimize G
pred_fake = self.netDisc(adv_images)
loss_G_fake = F.mse_loss(pred_fake, torch.ones_like(pred_fake, device=self.device)) #MSE
loss_G_fake.backward(retain_graph=True)- 对于第三部分Hinge Loss,不同于论文的实现.代码部分直接用$G(x)$的$L_2$范数作为损失函数.也许是效果更好 ?
# calculate perturbation norm
C = 0.1
loss_perturb = torch.mean(torch.norm(perturbation.view(perturbation.shape[0], -1), 2, dim=1))
# loss_perturb = torch.max(loss_perturb - C, torch.zeros(1, device=self.device))- 对于第一部分$L_{adv}$,这里给出的是不定向攻击的实现.使用真实类别的概率和其他类别中的最大概率之间的差值作为损失项.起到了拉低真实类别的概率(拉高其他类别的概率)的作用.这里独热编码和取出其他类别概率的最大值写的很好
# cal adv loss
logits_model = self.model(adv_images)
probs_model = F.softmax(logits_model, dim=1)
# 生成对角线矩阵,对于每行来说就是对应类别的独热编码,这里取出真实类别对应的掩码
onehot_labels = torch.eye(self.model_num_labels, device=self.device)[labels]
# C&W loss function
# 通过掩码得到模型预测的正确类别的概率值
real = torch.sum(onehot_labels * probs_model, dim=1)
# 这里*10000是让让真实类别对应的位置值很小,从而让max取不到(其实没什么必要吧,之前做了softmax了)
other, _ = torch.max((1 - onehot_labels) * probs_model - onehot_labels * 10000, dim=1)
zeros = torch.zeros_like(other)
# 衡量真实类别与其他类别的差距,如果<=0就负0
loss_adv = torch.max(real - other, zeros)
loss_adv = torch.sum(loss_adv)训练结果
首先训练目标模型,对于测试集accuracy可以达到99.38%

接下来训练AdvGAN,训练60个epoch后损失如下.其实D训练的很好,说明对抗样本隐蔽性做的不太行,$L_{adv}$不高,说明攻击效果应该是达到的.
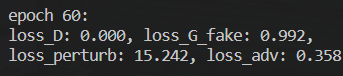
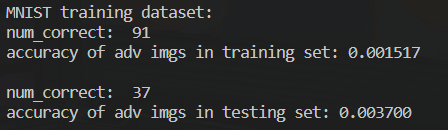
接下来使用对抗样本测试一下目标模型的accuracy.这里同样使用的测试集(增加扰动后).最后得到的准确率大约为0.3%(训练集的准确率是0.15%).好!
输出一下生成的对抗样本图像结束AdvGAN.(经典雪碧图)


评论