做了5题蓝桥杯中等题的JJJYmmm身心十分疲倦,决定入门一下生成式对抗网络(GAN).本次看的是开山之作: Ian Goodfellow的Generative Adversarial Nets
摘要
摘要指出本篇工作提出了一个新的框架,通过两个模型相互对抗来提高他们的生成(检测)效果.具体来说:一个是捕获数据分布(这个会在价值函数中体现)的生成模型G,还有一个是判断样本来自真实数据还是G的判别模型D.
G的训练目标是使D出错的概率最大化,最后希望达到的效果就是G生成的数据足够"以假乱真",D无法分别其真实性,在这种情况下,生成器G的分布$P_g=P_{data}$(P为概率密度函数),且D的输出恒为1/2.
这里的G/D可以简单都是用MLP,那么模型训练只需要反向更新即可,也不需要使用马尔科夫链或者近似推理网络.
GAN属于隐式生成网络,它不需要显示表示真实数据的分布$P_{data}$,这个分布蕴含在G中,我们只关注从这个分布采样出来的样本点即可,即G(z).
Introduction
引言基本是摘要的一个补充,主要谈了一下当时深度学习做生成模型效果不太好.之前做生成模型的思想主要是通过一些可学习参数去构造真实的数据分布$P_{data}$,这些参数通过调整尽量使$P_g=P_{data}$,调整的方式就是通过最大化对数似然函数.具体可以见我之前的博客~
本次提出的GAN则属于隐式生成模型,不需要知道$P_g$的具体形式,只需要最后检测模型D分不出来就可以了.
Related Work
讲了一下VAEs/NCE,还有jurgen在92年提到的predictability minimization.据说jurgen作为这篇论文的审稿人review很有意思~
Value Fuction V(G,D)
接下来就讲到价值函数啦,非常关键的一个地方.当然这里还需要对模型的输入进行进一步解释.
当G和D都是MLP的时候,GAN非常容易应用.首先是为了学习生成器在数据x上的分布$P_g$,先要定义输入噪声z的先验分布$p_z(z)$,然后通过MLP得到一个映射关系$G(z;\theta_g)$.接下来对于检验器D,MLP的映射$D(x,\theta_d)$输出一个向量,1表示x来自真实样本,0表示来自G.G的工作是让$log(1-D(G(z)))$尽可能小,而D的工作是让$log(D(x))$尽可能大的同时让$log(1-D(G(z)))$也尽可能大.根据上述描述可以得到价值函数V(G,D)
$$
\mathop{min}\limits_{G}\mathop{max}\limits_{D}V(G,D)=\mathbb{E}_{x\sim p_{data(X)}[logD(x)]} + \mathbb{E}_{z\sim p_{z(z)}log[1-D(G(z))]}
$$
GAN的训练过程见算法1,先k步迭代检测器D,在迭代生成器G.

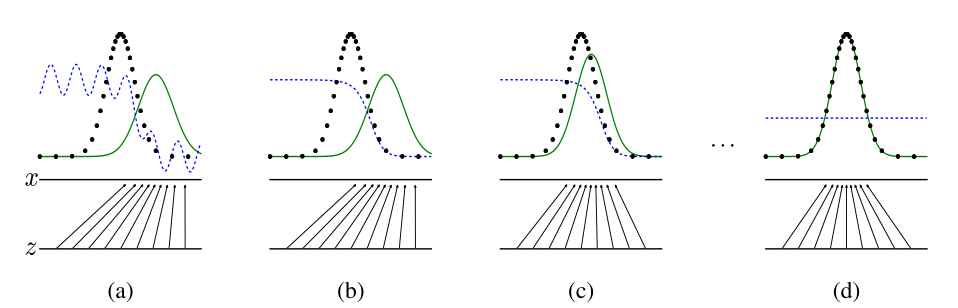
训练过程可以总结为一下四张图,假设数据x和噪声z都是一维向量.x的分布是灰色的正态分布,G(z)是绿色的正态分布,而检测器D是虚线.首先如图b训练D,它对x和g(z)做了一定区分;接下来训练G,让G(z)的分布曲线往x靠近,如图c.最后当两个分布曲线足够贴合时,检测器D无法分辩任何东西,所以是一条直线.
Theoretical Results
理论结果有两个:首先给出固定G的最佳辨别器$D^*$,其次是证明了价值函数的有效性.
Theorem 1.
对于固定的G,最佳分辨器$D^*$为
$$
D^*_G(x) = \frac{p_{data}(x)}{p_{data}(x)+p_g(X)}
$$
证明通过对V(G,D)进行变换得到,首先将g(z)换元成x
$$
\begin{align*}
V(G,D)&=\int_{x}p_{\mathrm{data}}(x)\log(D(x))d x+\int_{\cdot}p_{z}(z)\log(1-D(g(z)))dz\\
&=\int_{x}p_{\mathrm{data}}(x)\log(D(x))+p_{g}(x)\log(1-D(x)) dx
\end{align*}
$$
上式则可以转变成以下形式$\ y\to a\log(y)+b\log(1-y)$,其中a,b代表着data和G的数据分布,这个函数是凸函数,可以得到最优点时$y=\frac{a}{a+b}$.那么$D^*$得证
接下来我们可以把$D^*$带入V(G,D)中,得到
$$
\begin{align*}
C(G)&=\mathop{max}\limits_{D}V(G,D) \\ \\
&=\mathbb{E}_{x\sim p_{\mathrm{data}}}[\log D_{G}^{*}(x)]+\mathbb{E}_{z\sim p_{z}}[\log(1-D_{G}^{*}(G(z)))]\\ \\
&=\mathbb{E}_{x\sim p_{\mathrm{data}}}[\log D_{G}^{*}(x)]+\mathbb{E}_{x\sim p_{g}}[\log(1-D_{G}^{*}(x))]\\ \\
&=\mathbb{E}_{x\sim p_{\mathrm{{data}}}}\left[\log{\frac{p_{data}(x)}{p_{\mathrm{data}}(x)+p_{g}(x)}}\right]+{\mathbb{E}_{x\sim p_{g}}}\left[\log{\frac{p_{g}(x)}{p_{\mathrm{data}}(x)+p_{g}(x)}}\right]
\end{align*}
$$
接下来我们考虑在D*的情况下V(G,D)如何达到最小,即G也训练到极致,我们对刚刚的C(G)做如下变形,具体来说就是在分式那个地方乘1/2,使其也变成一个分布.(因为之前两个分布求积分结果是2,如果/2积分结果就是1,可以看成是一个新分布)
再根据KL散度的定义可以把C(G)表示成如下形式,KL>=0,取等条件就是两个分布相等,根据两个KL散度可以得到$p_g=p_{data}$时,C(G)有最小值$-log(4)$
$$
C(G)=-\log(4)+K L\left(p_{\mathrm{data}}\Big|\Big|\frac{p_{\mathrm{data}}+p_{g}}{2}\right)+K L\left(p_{g}\Big|\Big|\frac{p_{\mathrm{data}}+p_{g}}{2}\right)
$$
对于这种对称性的KL散度,我们还有一个名称称呼它:琴生-香农散度,所以C(G)进一步表示成如下
$$
C(G)=-\log(4)+2\cdot J S D\left(p_{\mathrm{data}}||p_{g}\right)
$$
Theorem 2.
第二个理论证明是假定在G/D具有充分能力的情况下,通过算法1,每次D都能迭代到D*.这样G最终可以使$p_g$收敛到$p_{data}$.这个主要是通过说明函数的凹凸性来证明的.具体来说就是把V(G,D)写成$p_g$的函数,即函数的函数,然后balaba....不是非常懂,直接贴原文了

Experiments
实验就是生成数字/人脸这些....没什么好说的(不过在当时应该算是效果挺好的吧)


评论