本节主要是学GAN的时候附带了解一下显式生成模型的基本原理~
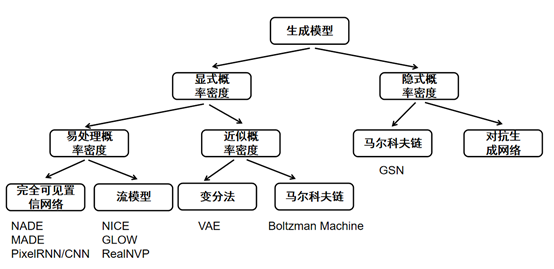
生成模型分为显式和隐式两种,显示就是具体求出(拟合)数据分布$P_{data}$,可以使用极大似然法.假设$P_g$是生成模型产生的数据分布,$\theta$是模型的参数.
首先对所有数据样本计算似然函数$L(\theta)$:
$$
L(\theta) = \prod_{i=1}^N{P_g(x^{(i)};\theta)}
$$
似然函数是一个关于模型参数$\theta$的函数,当选择不同的参数$\theta$时,似然函数的值是不同的,它描述了在当前参数下,使用模型分布$P_g(x;\theta)$产生数据集中所有样本的概率。一个朴素的想法是:在最好的模型参数$\theta_{ML}$下,产生数据集中的所有样本的概率是最大的,即
$$
\theta_{ML}=argmaxL(\theta)
$$
但实际在计算机中,多个概率的乘积结果并不方便储存,例如计算过程中可能发生数值下溢的问题,即对比较小的、接近于0的数进行四舍五入后成为0。我们可以对似然函数取对数来缓解该问题,并且仍然求解最好的模型参数使对数似然函数最大,即
$$
\theta_{ML}=argmax \sum_{i=1}^Nlog[P_g(x^{(i)};\theta)]
$$
可以发现,使用极大似然估计时,每个样本$x_i$都希望拉高它所对应的模型概率值$P_g(x^{(i});\theta)$,如图所示,但是由于所有样本的密度函数的总和必须是1,所以不可能将所有样本点都拉高到最大的概率;一个样本点的概率密度函数值被拉高将不可避免的使其他点的函数值被拉低,最终将达到一个平衡态。
对于刚刚的$log$和,我们可以除以$N$,那么$\theta_{ML}$的含义就是尽可能达到经验分布$\hat{P}_{data}$下样本概率对数的期望值.
$$
\theta_{ML}=argmax\space\mathbb{E}_{\hat{P}_{data}} log[P_g(x^{(i)};\theta)]
$$
还有一种对极大似然估计的理解:最小化训练集上的经验分布$\hat{P}_{data}(x)$和模型分布$P_g(x;\theta)$之间的KL散度值(这个在之前的机器学习里也提到过),即
$$
\theta_{ML}=argminD_{KL}(\hat{p}_{data}||P_g)
$$
KL散度的表达式是
$$
D_{KL}(\hat{p}_{data}||P_g) = \mathbb{E}_{\hat{P}_{data}}[ log\hat{p}_{data}(x)-logP_g(x;\theta)]
$$
因为第一项与$\theta$无关,所以可以写成
$$
\theta_{ML}=argmax \sum_{i=1}^Nlog[P_g(x^{(i)};\theta)]
$$
可以发现两者是完全一样的,也就是说极大似然估计就是希望$P_g$和$P_{data}$尽量相似,最好相似到无任何差异(KL散度值为0),这与生成模型的思想是一致的。但实际的生成模型一般不可能提前知道$P_g$的表达式形式而只需要估计表达式中的参数,实际中的生成模型非常复杂,往往对$P_g$无任何先验知识,只能对其进行一些形式上的假设或近似。

评论