TSNE降维

基本概念

t-SNE(t-distributed stochastic neighbor embedding)是用于降维的一种机器学习算法，由 Laurens van der Maaten 等在08年提出。

t-SNE 是一种非线性降维算法，非常适用于高维数据降维到2维或者3维，进行可视化。该算法可以将对于较大相似度的点，t分布在低维空间中的距离需要稍小一点；而对于低相似度的点，t分布在低维空间中的距离需要更远。

tips1:TSNE将数据点之间的相似性转换为联合概率，并试图最小化低维嵌入和高维数据的联合概率之间的Kullback-Leibler差异。t-SNE的成本函数不是凸的，即使用不同的初始化，我们可以获得不同的结果。

tips2:如果特征数量非常多，强烈建议使用另一种降维方法（例如，对于密集数据使用PCA或对于稀疏数据使用TruncatedSVD）将尺寸数量减少到合理的数量（例如50个）。这将抑制一些噪声并加快样本之间成对距离的计算。

tips3:sklearn TSNE 源码

tips4:t-SNE 原理及Python实例 - 知乎 (zhihu.com)

优缺点

优点：

• 对于不相似的点，用一个较小的距离产生较大的梯度来排斥区分。
• 这种排斥不会无限大(梯度中分母)，避免不相似的点距离太远。

缺点：

• 主要用于可视化，很难用于其他目的。比如测试集合降维，因为他没有显式的预估部分，不能在测试集合直接降维；比如降维到10维，因为t分布偏重长尾，1个自由度的t分布很难保存好局部特征，可能需要设置成更高的自由度。
• t-SNE倾向于保存局部特征，对于本征维数(intrinsic dimensionality)本身就很高的数据集，是不可能完整的映射到2-3维的空间（映射存在信息损失）
• t-SNE没有唯一最优解，且没有预估部分。如果想要做预估，可以考虑降维之后，再构建一个回归方程之类的模型去做。但是要注意，t-sne中距离本身是没有意义，都是概率分布问题。
• 训练太慢。有很多基于树的算法在t-sne上做一些改进

算法流程

• 首先在高维空间,将样本之间的距离转换成概率分布.

$$
P_{j|i}=\frac {exp(-||x_i-x_j||^2/2\sigma^2)}{\sum_{k \neq i} exp(-||x_i-x_k||^2/2\sigma^2)}
$$

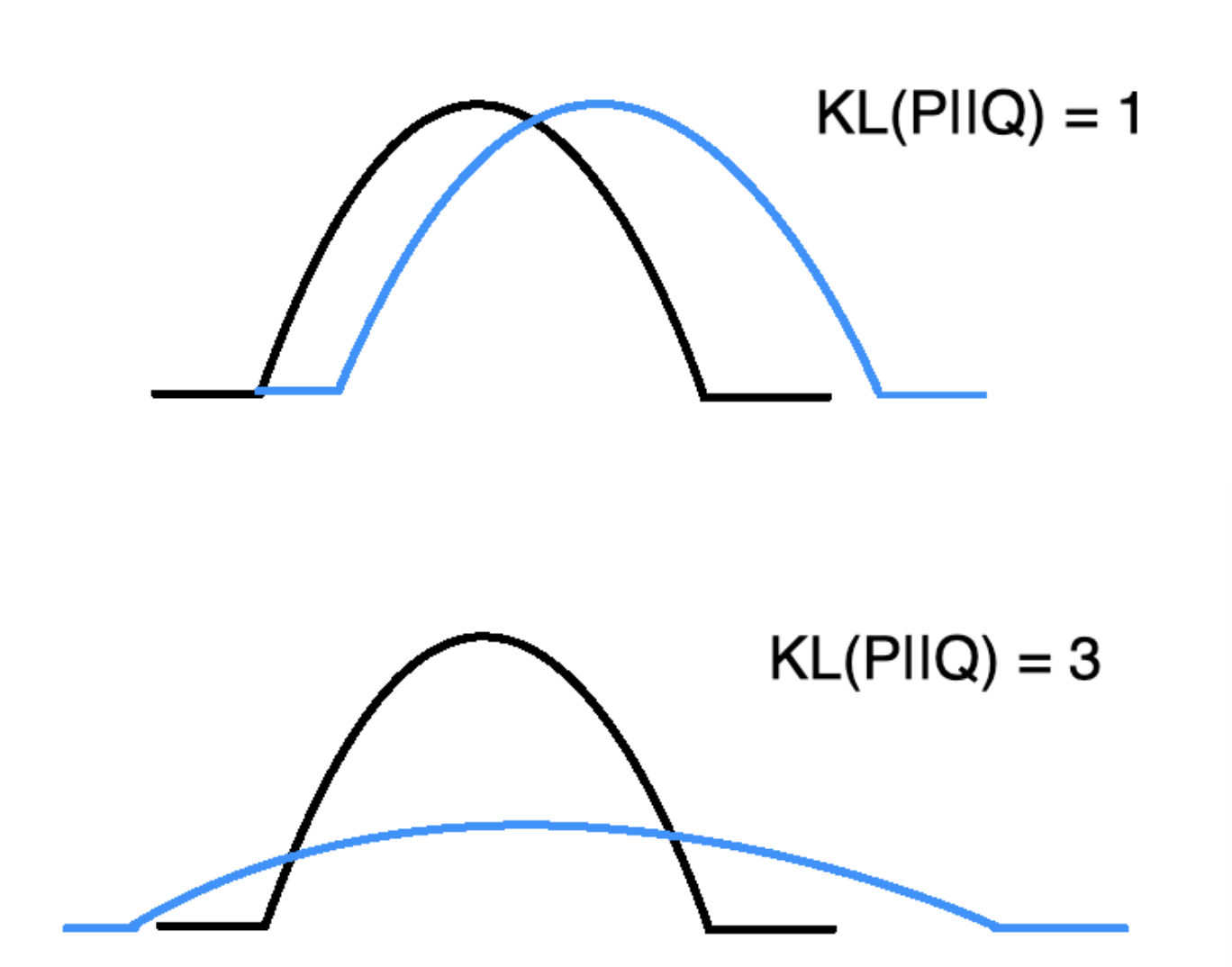
• 在低维空间寻找类似的概率分布,并使用KL散度衡量高维空间/低维空间两概率分布的相似度.

• 使用梯度下降最小化所有数据点上的KL散度总和
  $$
  C = \sum_i KL(P_i||Q_i)=\sum_i \sum_j p_{j|i} \log {\frac {p_{j|i}}{q_{j|i}} }
  $$

• 对 C 求偏导数(每个样本)获得每次更新的方向

sklearn

• n_components : tsne最终降维的维度
• init : 初始化方法,可以使用pca or random

from sklearn.manifold import TSNE
tsne=TSNE(n_components=1,init='pca', random_state=501)
down_X = tsne.fit_transform(X) # train and get embadding