基本概念
- DBSCAN:Density-Based Spatial Clustering of Applications with Noise (具有噪声的基于密度的聚类方法)
- 核心对象:若某个点内的密度达到算法设定的阈值则为核心点
- ∈-邻域的距离阈值:设定的半径r
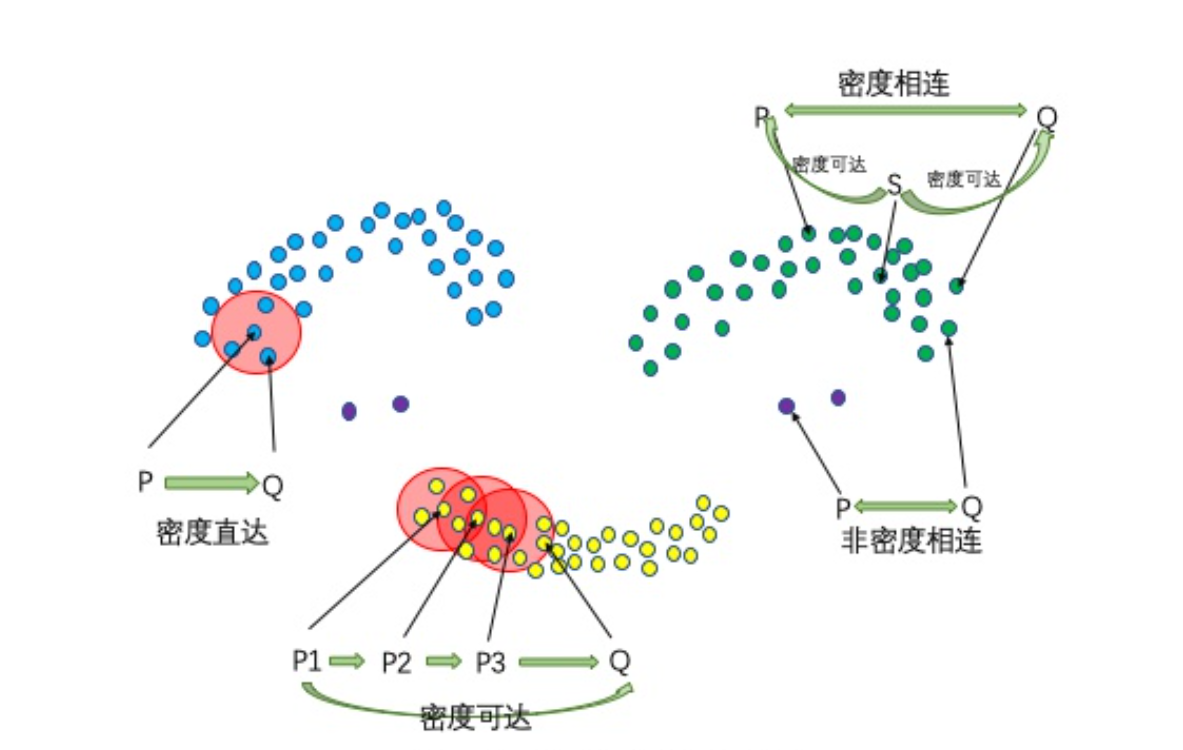
- 直接密度可达:若点p在点q的r邻域内,且q是核心点则p-q直接密度可达
- 密度可达:若有一个点的序列$q_0,q_1,...,q_k$,对任意$q_i,q_{i-1}$直接密度可达,那么称$q_0,q_k$密度可达。即直接密度可达的‘传播’。
- 密度相连:若从核心点p出发,点q和点k都是密度可达的。那么点q和点k是密度相连的。(不要求q/k必须是核心点)
- 边界点:属于某个类的非核心点
- 噪声点:不属于任何一个类簇的点,从任何一个核心点出发都是密度不可达的。
参数选择
-
半径∈:可以根据K距离设定,即寻找突变点。
-
K距离:给定数据集P = {p(i);i=0,1,...,n},计算点p(i)到集合D的子集S中所有点之间的距离d,按照距离从小到大排序,d(k)即K距离
例如点s到其他点的距离数组$d_k$={0.1,0.11,0.12,0.3,0.5....}(已排序),发现前三个距离相差不大,第四个距离0.3发生突变,那么半径取d(3)=0.12,MinPts取3
-
MinPts:K-距离中的K值,一般从小开始取
优缺点
优点:
- 可以处理任意形状的簇
- 不需要指定簇的个数
- 擅长找到离群点,用于异常检测任务
缺点:
- 高维数据处理困难(可以寻找降维方法)
- 半径r和MinPts难以确定
- 算法效率慢
算法流程
伪代码如下,类似宽度优先搜索进行簇的传播:
bool visited[n];
memset(visited,false,sizeof visited);
while(some point is unvisited){
choose p randomly which is unvisited;
if(p ∈-field has more that MinPts points){
create a new cluster C;
N = {q in p ∈-field};
for(auto &q:N){
if(visited[q]==false){
visited[q] = true;
if(q ∈-field has more that MinPts points){
add {k in q ∈-field} to N;
}
add q to cluster C;
}
}
}else{
add p to noise;
}
}可视化
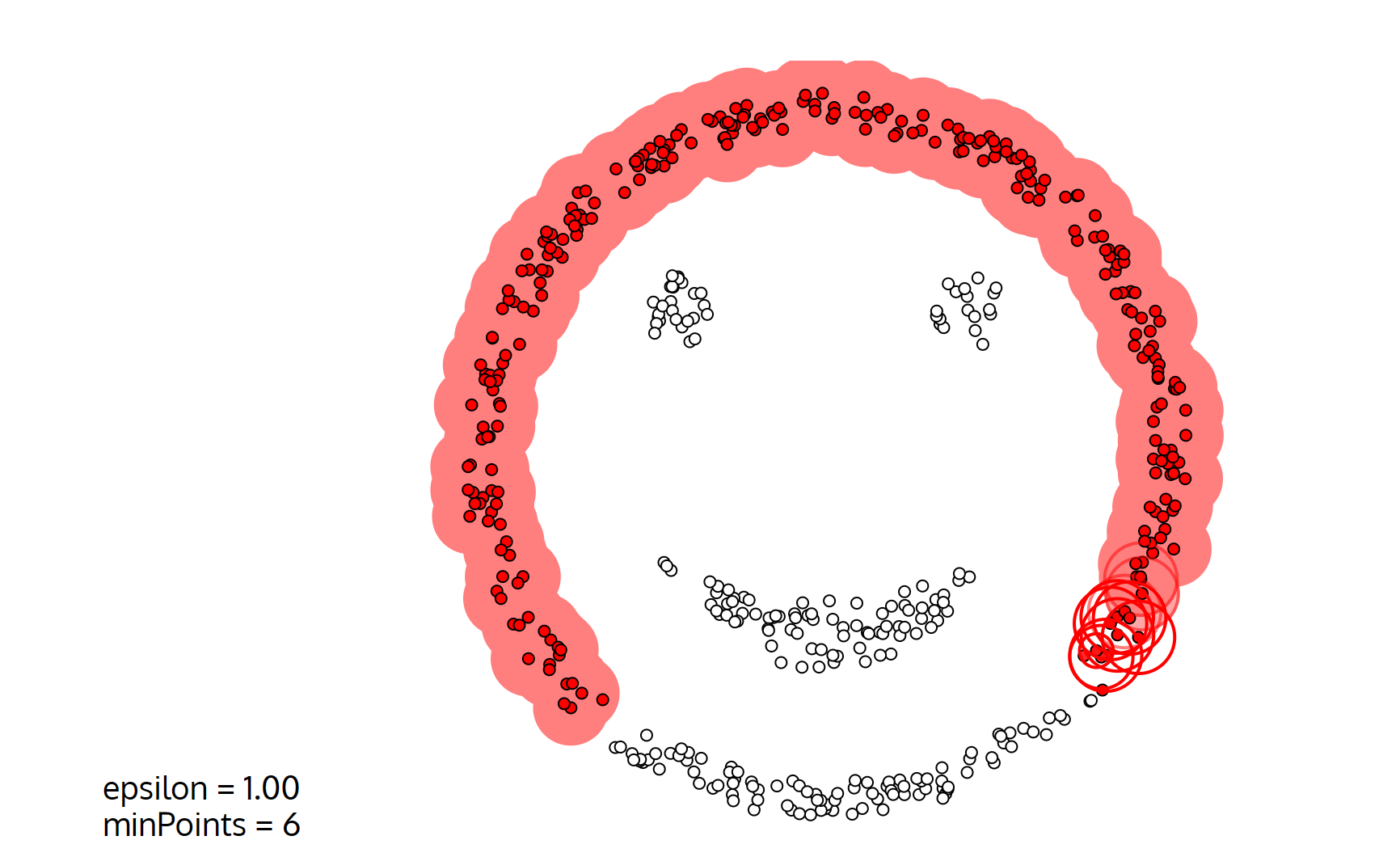
sklearn
from sklearn.cluster import DBSCAN
dbscan = DBSCAN(eps=0.5,min_sample=5)
dbscan.fit(X) # train
dbscan.label_ # label label=-1 means noise
descan.core_sample_indices_ # 核心样本在原始训练集中的位置
评论