KMeans聚类 - Axuanz的学习日记

聚类概念

属于无监督学习(无标签)
顾名思义，就是将相似的东西分到一组
难点在于如何评估聚类效果以及调整参数

基本概念

K代表最后需要得到的簇个数(比如二分类K=2)
一个簇的质心计算：采用均值，即每个特征向量取平均值
距离度量：经常使用欧几里得距离和余弦相似度(高维特征最好先执行一次标准化)
优化目标：实现$min\sum_{i=1}^{k}\sum_{x∈C_i}dist(C_i,x)^2$

优缺点

优点：

算法简单、快速
适合常规数据集(就是一坨一坨的那种，没有特定形状)

缺点：

K值难以确定(一般是遍历K值取Inertia的拐点)
算法复杂度与样本呈线性关系(一次迭代)
很难发现任意形状的簇，比如二维特征的样本，一个圆环套一个球的形状KMeans就很难检测出来。

算法流程

首先随机选取K个样本作为K个簇的中心(在KMeans++中，使用最大距离进行初始化)
- KMeans++逐个选取K个簇中心，且离其它簇中心越远的样本点越有可能被选为下一个簇中心
将每个样本分配到K个簇中，具体选择哪个簇取决于该样本和K个簇的距离，选择距离最近的簇(分配样本)
此时所有样本都分配到对应的簇，在每个簇中更新簇中心。新的簇中心采用简单的均值计算(更新簇中心)
回到第二步再次分配样本，直到达到迭代次数上限或损失指标小于某个阈值(损失指标有inertia/轮廓系数)

KMeans代码实现

import numpy as np
class KMeans:
    def __init__(self,data,num_clusters):
        self.data = data
        self.num_clusters = num_clusters

    def train(self,max_iterations):
        # 1.choose k centers
        centroids = KMeans.centroids_init(self.data,self.num_clusters)
        # 2.begin train
        num_examples = self.data.shape[0]
        closest_centroids_ids = np.empty((num_examples,1))
        for _ in range(max_iterations):
            # 3.get closest center id
            closest_centroids_ids = KMeans.centroids_find_closest(self.data,centroids)
            # 4.update k centers
            centroids = KMeans.centroids_compute(self.data,closest_centroids_ids,self.num_clusters)
        return centroids,closest_centroids_ids

    @staticmethod
    def centroids_init(self,data,num_clusters):
        num_examples = data.shape[0]
        random_ids = np.random.permutation(num_examples)
        centroids = data[random_ids[:num_clusters],:]
        return centroids

    @staticmethod
    def centroids_find_closest(self,data,entroids):
        num_examples = data.shape[0]
        num_centroids = centroids.shape[0]
        closest_centroids_ids = np.zeros((num_examlpes,1))
        for example_index in range(num_examples):
            distance = np.zeros(num_centroids,1)
            for centroid_index in range(num_centroids):
                distance_diff = data[example_index,:] - centroids[centroid_index,:]
                distance[centroid_index] = np.sum(distance_diff**2)
            closest_centroids_ids[example_index] = np.argmin(distance)
        return closest_centroids_ids

    @staticmethod
    def centroids_compute(self.data,closest_centroids_ids,self.num_clusters):
        num_features = data.shape[1]
        centroids = np.zeros((num_clusters,num_features))
        for centroid_id in range(num_clusters):
            closest_ids = closest_centroids_ids == centroid_id
            centroids[centroid_ids] = np.mean(data[closest_ids.flatten(),:],axis=0)
        return centroids

sklearn

接下来介绍sklearn库中的KMeans实现.

文档见sklearn.cluster.KMeans — scikit-learn 1.2.2 documentation

`Attributes`

`init`

n_clusters : 簇个数K
random_state : 随机数种子
init : K个簇中心的初始化方式
n_init : 算法执行次数,取结果最好的一次
max_iter : 单次算法迭代次数(分配簇/更新簇)

from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=2,random_state=0,init='k-means++',n_init=10,max_iter=300)

`fit`

kmeans.fit(X) # input X
kmeans.cluster_centers_ # center coordinate
kmeans.label_ # every sample's label
kmeans.inertia # loss

`pred`

kmeans.predict(New_X)
kmeans.label_

`tranform`

Transform(): Method using these calculated parameters apply the transformation to a particular dataset.

返回值shape : (num_examples,num_clusters) 即每个样本和每个类的距离通过这个方法也可以得到predict结果(argmin)

from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
sc.fit_tranform(X_train)
sc.tranform(X_test) # 一定是tranform 保证train和test使用同一个转化标准

可视化

# draw cluster points
def plot_data(feature,snr,label):
    df = pd.DataFrame(dict(x=snr, y=feature, color=label))
    fig, ax = plt.subplots()
    colors = {0:'red', 1:'blue'}
    ax.scatter(df['x'], df['y'], c=df['color'].apply(lambda x: colors[x]))
    plt.show()

# draw cluster centers
def plot_centriods(snr,centroids,weights=None,circle_color='g',cross_color='k'):
    if weights is not None:
        centroids = centroids[weights>weights.max()/10]
    plt.scatter(snr,centroids[:],
               marker='o',s=30,linewidths=8,
               color=circle_color,zorder=10,alpha=0.9)
    plt.scatter(snr,centroids[:],
               marker='x',s=50,linewidths=50,
               color=circle_color,zorder=11,alpha=1)

评估指标

inertia指标

inertia : 每个样本距离质心的距离

score方法的结果是inertia的负值(绝对值越大分数越小)

kmeans.inertia_
X_dist = kmeans.transform(X)
np.sum(X_dist[np.arange(len(X_dist)),kmeans.labels_]**2) # inertia计算
kmeans.score(X) == -1*kmeans.inertia_

轮廓系数

某个样本的轮廓系数定义为:
$$
s = \frac {disMean_{out} - disMean_{in}}{max(disMean_{out}-disMean_{in})}
$$
其中$disMean_{in}$为该点与本类其他点的平均距离，$disMean_{out}$为该点与非本类点的平均距离。该值取值范围为[−1,1]，越接近1则说明分类越优秀。在sklearn中函数 silhouette_score()计算所有点的平均轮廓系数，而silhouette_samples()返回每个点的轮廓系数。

K值选取(拐点法)

kmeans_per_k = [KMeans(n_clusters=k).fit(X) for k in range(1,10)]
inertias = [model.inertia_ for model in kmeans_per_k]
# draw fig
plt.figure(figsize=(8,4))
plt.plot(range(1,10),inertias,'bo-')
plt.show()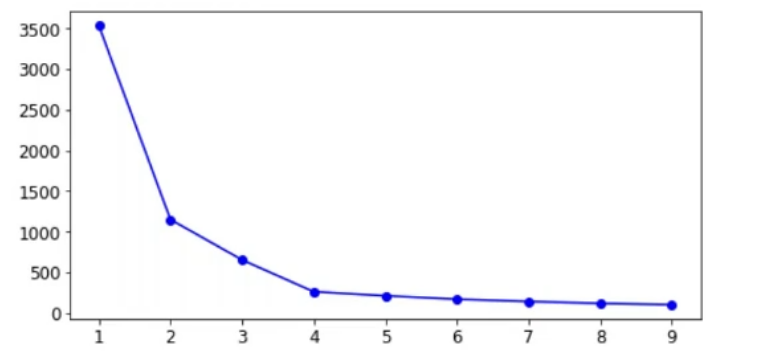

半监督学习

KMeans也可以用于半监督学习。

比如在一个少样本训练场景下，相比于随机选取50个训练样本打标加入训练这种方式，可以先使用聚类挑出50个簇中心，每个簇选取一个样本作为典型样本；用这些样本打标训练，最后测试出来的acc会更高。除此之外，还可以通过标签传播(同一个簇内的标签一致)的方式扩大训练集。