年前分享一篇关于Sequence Packing的论文:2107.02027
笔者认为Packing是Transformer架构训练时一个比较比较核心的问题(应用也非常广泛,LLMs如Llama 3会拼接多个文档做上下文的拓展),因为Transformer一般有一个固定的Context Size S,所有样本都需要pad到S的长度,从而满足transformer的矩阵计算;而pad token是不参与loss计算的,所以这里就带来了Context的浪费;对于一些分布很极端的数据集如Wikipedia,一个epoch下来,pad token要占到所有训练token的50%。
在以上背景下,有两种可以解决pad token过多带来的计算损耗。一个是优化计算流程,使pad token不参与attention这样复杂度高的计算,但是这种方法往往需要非常工程的优化;另一个是降低pad token的比例,也就是所谓的Sequence Packing了——把多个样本或序列拼在一起。
Packing带来的好处是非常明显的:多个样本拼在一起,首先减少了样本数,其次单条数据中有效token的比例也增加,这些优点加快了模型的收敛。
那么如何确定packing的逻辑呢?如果考虑全局最优(优化目标是pad token最少),这个问题其实就是装箱问题,NP hard。所以我们能承受的一般是启发式等近似算法。接下来介绍论文里提到的两个Packing Strategy。
Non-Negative Least Squares Histogram-Packing(NNLSHP)
NNLSHP利用了训练数据分布的直方图信息进行最小二乘法求解Packing逻辑。
首先,给定Context Size S,它先定义了一系列Packing的组合。例如 S = 512 = 256 + 128 + 128。一条512的数据可以通过拼接一条256的数据和两条128的数据得到。这个组合其实就是所谓的Partition Number (谢谢欧拉)。为了减少组合数,算法定义一条数据最多由N条数据打包到一起。得到所有的组合之后,可以排布成一个矩阵。
其中每一行代表某一个长度的数据,每一列代表一种策略,列和小于等于N。例如对于S = 8,N = 3,Strategy Matrix如下图。总共有10种策略,第一种就是两个长度为1的数据和长度为6的数据拼在一起,得到一条长度为8的新数据。
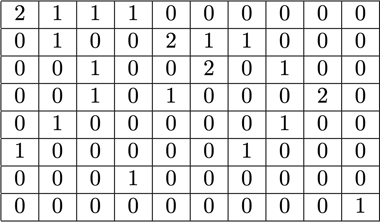
得到这个Matrix后,整个数据集的分布我们也是知道的,即每个长度的数据各自有多少条,我们记为b;每个策略应该应用多少次,我们记为x。那么x可以通过求解Ax=b得到。
得到x之后,我们就可以愉快的进行Packing了。当然这边有一些细节,例如x按照定义应该都是正整数,但是实际应用时只要按照$x \geq 0$计算再舍入即可(这就是算法名字中的NN)。
Shortest-Pack-First Histogram Packing
第一个算法还是存在一些缺点,首先预设了每条数据最多由三条数据Pack得到,其次Strategy Matrix随着S增大也增大,在超长上下文时计算效率太低。所以我们希望可以把这个痛点解决,于是乎启发式的SPFHP来了~
其实内容只需要三行就可以解释清楚:
- 这个算法运行在数据分布直方图上,从长序列往短序列遍历
- 检查当前长度能不能和前一个长度进行合并,如果不能,那么他们单独占一个样本位置
- 如果可以(或者部分可以),那么和前一个长度进行合并,并更新直方图的信息
例如下图S = 8的情况;从8遍历到3,此时长度为3的数据可以和长度为4的数据进行合并,组成长度为7的四条数据
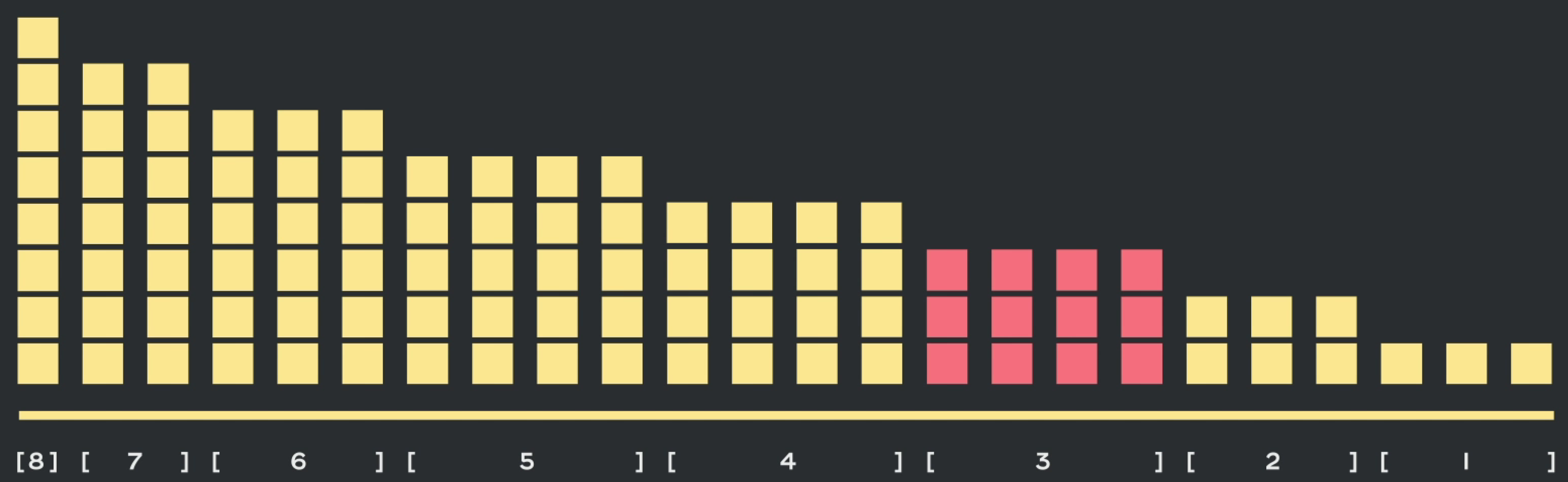
接着长度为2的数据可以和长度为5的数据进行拼接,组成长度7的数据
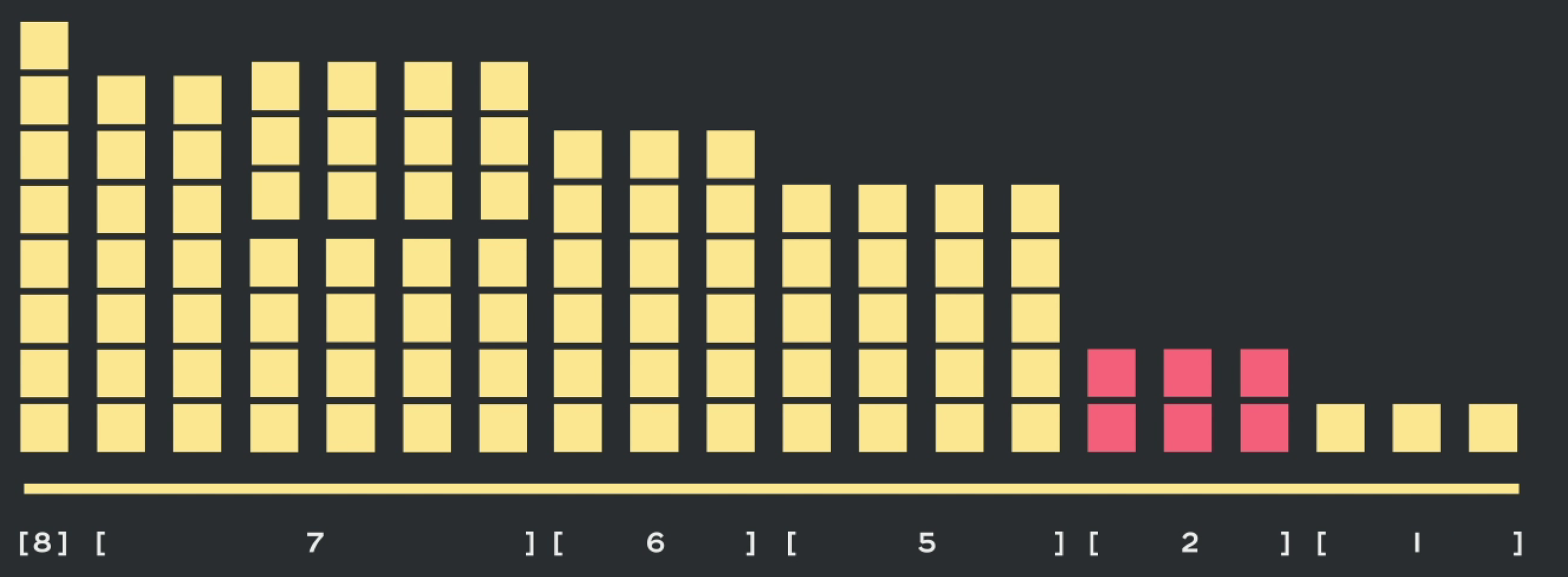
最后三个长度1的数据分别和5、6的数据进行合并
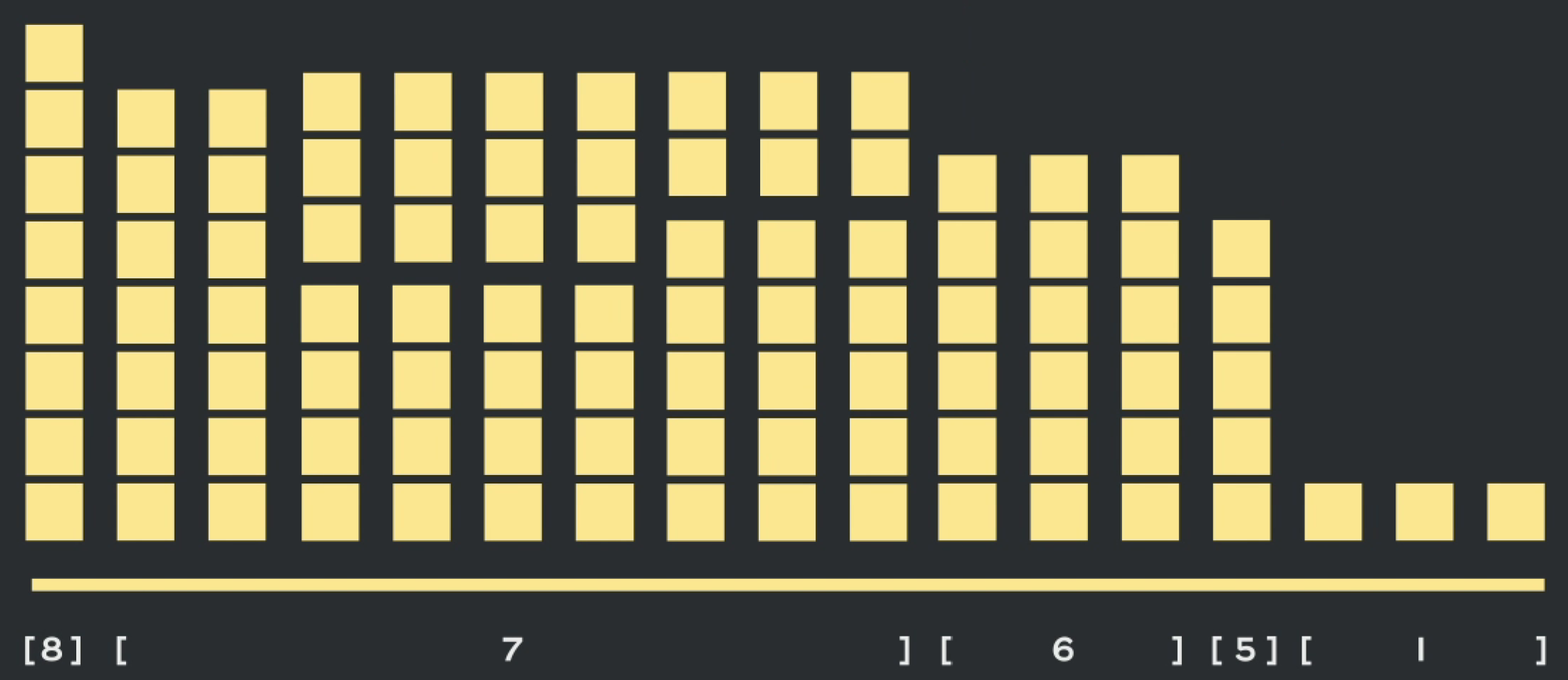
最终得到的合并序列如下,对于一些空位,再填入pad token。

这个算法运行复杂度是O(S),因此速度非常快。值得注意的是每次合并时,选择的是前一个长度的数据进行合并,也就是说,每次合并保证预留出来的空间最多。这个和传统的First-Fit或者磁盘管理中的最佳适应是不太一样的,最佳适应是要求剩余空间尽可能少,而这里是尽可能多。
论文里也解释了:两种策略从最终效果来说相差不大,而First-Fit复杂度更高,因此选择了short-Fit。复杂度高是因为这里多了一步二分查找的过程。
2025第一篇博客,Hello

评论