http://arxiv.org/abs/2305.14314
Quantization + LoRA,了解一下呢。
LoRA之前写过博客了,这里主要想说一些如何与量化结合起来,以及用到的一些新的tech
当然像分页优化这种就掠过了...需要用到Nvidia统一内存去做内存/GPU交换,cuda编程不会捏,感兴趣可以看论文附的链接https://docs.nvidia.com/cuda/cuda-c-programming-guide/
4-bit NormalFloat(NF4)
之前谈量化说到INT8/INT4,是把浮点数量化成定点数。量化操作一般是除去一个量化因子$s = \frac {2^{N-1}} {ABSMAX}$,这个其实潜在地假设了数据满足的是均匀分布,实际上LLM权重满足的是一个正态分布。
那么NF4就把概率作为量化间隔,而不是把实际的数值差作为量化间隔。看以下这个图就明白了。p满足等差数列,而X明显不满足,越近0,X的分布越密集。
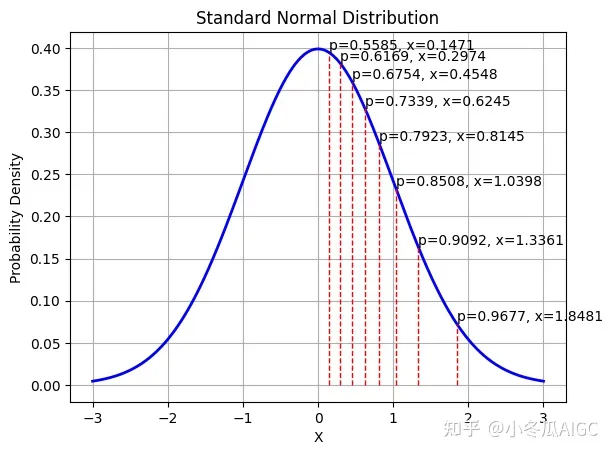
这个时候把X归一化到到[-1,1],得到的就是quant book啦。那么实际应用中怎么量化呢,其实和传统量化差不多,输入数据首先除一个ABSMAX,归一化到[-1,1],然后查quant book,最靠近的那个浮点数就是对应的量化等级了。(反量化的时候直接取quant book对应的那个浮点数即可)
NF4的quant book是['-1.0000', '-0.6962', '-0.5251', '-0.3949', '-0.2844', '-0.1848', '-0.0911', '0.0000', '0.0796', '0.1609', '0.2461', '0.3379', '0.4407', '0.5626', '0.7230', '1.0000']
这种量化方案考虑了输入本身的分布(权重近似正态分布),bin划分的更合理,自然会减少一定的量化误差啦。
Double Quantization
双重量化,顾名思义就是执行两次量化。
回顾传统量化,对于一个权重矩阵W,为了更好的表示它,一般会对它进行per-channel的量化,即把W分成n块,每一块对应不同的量化因子s,量化后,我们不仅要保存量化后的权重W‘,还要保存这n个量化因子(因为反量化的时候要用),而且量化因子一般和W的类型一样,例如同样是FP32。
那么为了保证量化质量,这个n可能很大,比如和W的channel数相当,那么量化因子的保存就会是一笔比较大的内存开销。所以!Double Quantization就是量化量化因子,让它占的内存少一点!
开始小小的实例分析(其实是论文里附带的例子)。
对于FP32的W,我们决定把它量化成INT4,块大小取64(总共$numel(W)/64$块),那么相当于W中的每64个参数会共享一个FP32量化因子s,那么每个参数对应的量化因子bit数是$32/64=0.5$。
如果我们对量化后的因子再次量化,将其量化到8bit,块大小选择256(这里指每256个量化因子共用一个FP32量化因子,有点绕哈哈哈哈),那么这个时候我们得到了一个新的量化因子s'(FP32),和一个量化后的INT8量化因子q(s),这个时候再来计算下W每个参数对应的量化因子bit数,首先第一次量化的块大小是64,即W中64个参数共用一个量化因子s,s又被量化到了8bit,所以是$8/64$,我们还要保存量化s的量化因子s’,这个s‘被256个s共用,每个s又被W中64个参数共用,那么一个s'被64*256个W参数共用,那么就是$32/(64 \times 256)$,最后每个参数对应的量化因子bit数是$8/64 + 32/(64 \times 256) = 0.127$,比传统量化减少了0.373bit/per param。
QLoRA
介绍完前面两个,QLoRA的训练用以下公式就一目了然了。forward过程W会反两次量化从NF4到BF16,和同为BF16的X做运算;backward的时候只对$L_1, L_2$进行更新(即LoRA里的A,B)

doubleDequant就是我刚刚提到的两次反量化啦。先反量化W的量化因子s,再用恢复后的量化因子反量化W。


评论