如何偷到闭源LLM的Hidden-Dimension

挺有意思的一篇论文 Stealing Part of a Production Language Model(arxiv2403.06634)，给出了一种通过black-box API查询来恢复LLM投影矩阵的方法。实际意义嘛...可以拿来蒸馏？但是成本还挺高的（

同期工作 Logits of API-Protected LLMs Leak Proprietary Information arxiv/2403.09539

简单讲一下Algorithm 1(其他的看不懂

这里假设攻击者的能力是可以拿到LLM的Logit-Vector API，也就意味着可以拿到每个token对应的logits，注意这里还没有过softmax，所以算法里没有考虑softmax的影响。这个假设其实很强，之后会慢慢放开到目前商用的API。

假设LLM的hidden-dim是$h$，词表大小是$l$。那么我们可以假设一个$n$，也就是查询API的次数，我们希望它比$h$要大。每次查询，我们输入LLM随机的前缀作为Prompt，那么我们会拿到一个长为$l$的logit-vector。

虽然论文里没讲，但这里的logits应该是指prompt最后一个token对应的logits

虽然logits长度为$l$，但是它们应该都在$dim = h$的子空间中，因为logits是通过一个hidden_states($dim = h$)乘上一个投影矩阵($h$x$l$)得到的。

因此，如果查询次数足够多，那么之后得到的logits响应会和之前的线性有关，这就给了我们分析的空间。

回到Algo. 1中的Q，因为Q的每行都是一个logits响应，它们处在维度为h的子空间，而子空间最多只有h个向量彼此线性无关，所以有$Rank(Q) \le h$。当n足够大时，$Rank(Q) = h$。

这里我省掉了论文里的$Q = WH$，因为作者应该是默认W一般是满秩的，不影响秩的计算。

那么现在求解h的方法就转向求解$Rank(Q)$，一般来说求一下奇异值个数count就可以了。

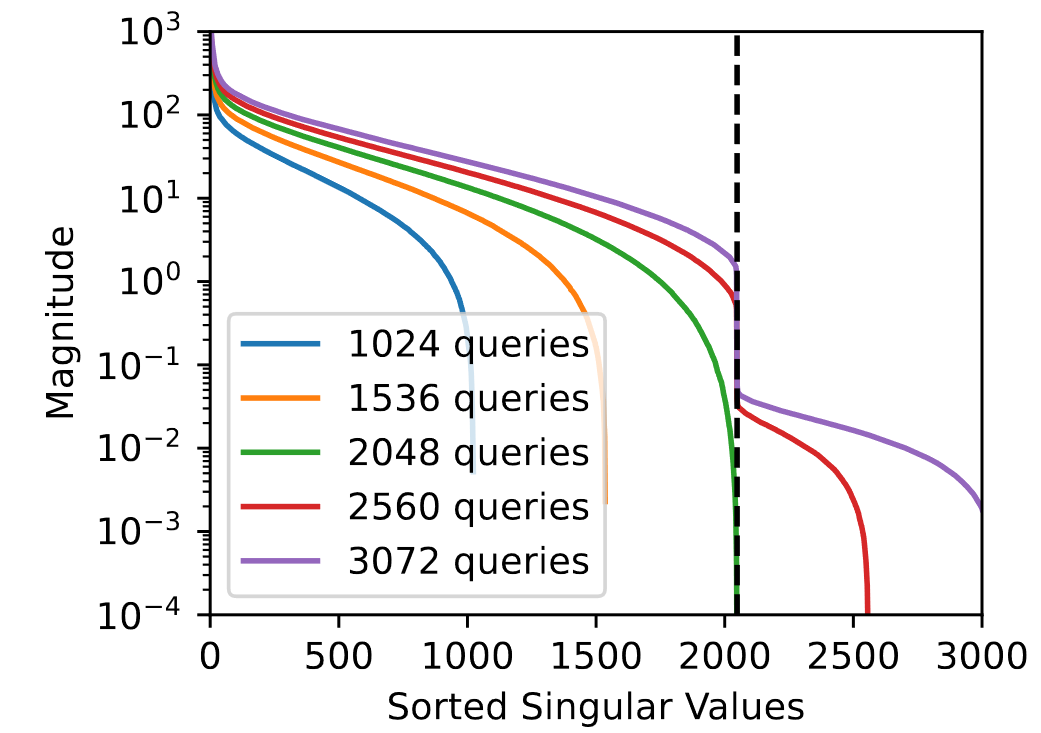
不过Q由logits组成，即浮点数矩阵，所以求解奇异值的时候会出现一些数值很小的假奇异值。于是作者这里在求解奇异值之后，sort了一下并通过$log ||\Delta||$筛选出真正的奇异值的个数。

以下是对Pythia 1.4B的hack，可以看到查询足够多的情况可以观察到一个明显的gap，从而确定hidden dimension是2048。

n < h时，$Q$是满秩的，且有n个非平凡奇异值，所以无法恢复出h