为什么开始看量化了,我也不知道
量化原理
我们一般谈LLM的精度,会涉及到FP32,FP16,BF16,INT8,INT4等字样。这些字段确定了LLM中一个参数所占的内存空间(如FP32指4字节浮点数,FP16和BF16指2字节浮点数,其中BF具有更多的指数位,INT8/4分别占8/4个比特)。其中INT8/4就涉及了模型量化,一个浮点数如何量化成一个定点数,这是量化干的最基本的事儿。
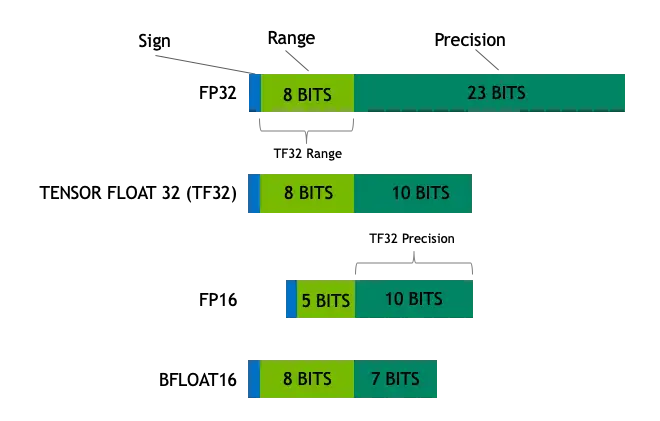
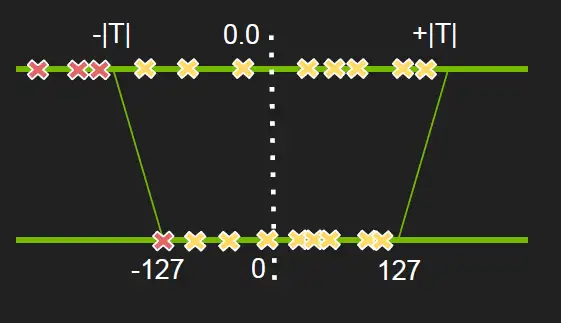
最直观的想法就是一组浮点数除去他们的ABS MAX,这些参数就落在了[-1,1]之间,然后根据量化位数N的不同乘以对应的步长$2^{N-1}$,接下来得到的数就是量化结果啦。
但上面这个问题在于浮点数的分布不均时,量化空间会有所浪费,所以实际应用时会进行一定的截断。
量化结束后,这组浮点数(weight/activation)就以定点数的形式存了下来。那么如何利用量化后的权重/激活呢?我们知道量化的时候一个浮点数先除了一个ABS MAX,再乘了一个$2^{N-1}$,那么$2^{N-1}/MAX$就是一个$\Delta$,我们实际做运算的时候额外把这个数除一下就可以了,比如$WX = \frac {\Delta W} {\Delta} X= \frac {Q(W)} {\Delta} X$。
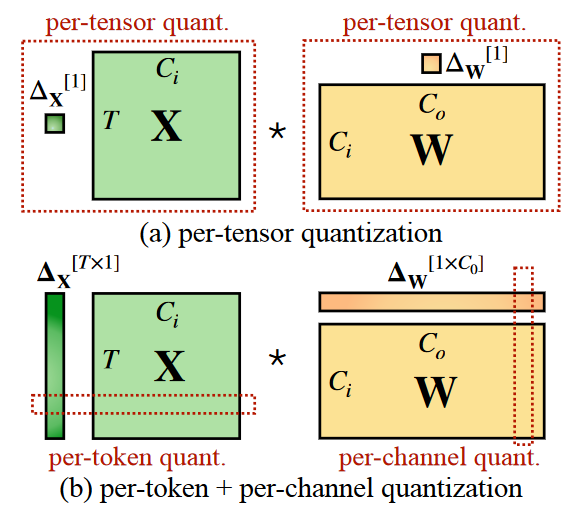
解决完量化/反量化的问题,下一个问题是如何给浮点数分组,全部用一个$\Delta$肯定不是好方法,SmoothQuant总结了一个很好的图,红色框线的区域代表用了同一个$\Delta$。per-tensor很好理解,很适合并行化,但是量化效果可能不好,比如X的不同channel具有不同的值域。per-token和per-channel就比较合适,在一个token/channel内进行量化。
但是为什么X应用
per-token,W应用per-channel呢?不能反过来?这其实是处于性能考虑。实际计算的时候,假如X,W都进行量化,那么矩阵乘法计算如下,可以看到反量化过程会涉及X,W的两个scale因子
如果想进一步优化速度,我们当然是希望提出两个scale,这样$x_q$和$w_q$两个量化后的结果就可以愉快地做乘法,对于整个XW也意味着可以先做INT8的矩阵乘法,而不是FP32/16的MM,两个scale只要在INT8矩阵乘法后做一个element-wise的乘法即可。说了这么多好处,提出两个scale的条件是与k无关,那么也就意味着,不同k之间的scale是一样的,也就对应
per-token和per-channel了~
这部分内容来自 arxiv2004.09602
说到这里,其实量化的理论基础就讲完了(吗
感觉量化还是更偏底层系统的方向,实现难难的
SmoothQuant
SmoothQuant的motivation是他们发现LLMs某些层产生的activation(上图中的X)在某些通道(col)上非常大,这导致了量化难度的增加,因为目前为了硬件实现效率,大家对于X的量化基本都是per-token,无法处理某些channel的outlier。而对于权重W,一般相对activation来说更加平坦,更容易量化。
在这个背景下,SmoothQuant提出可以把量化难度从X转移到W。
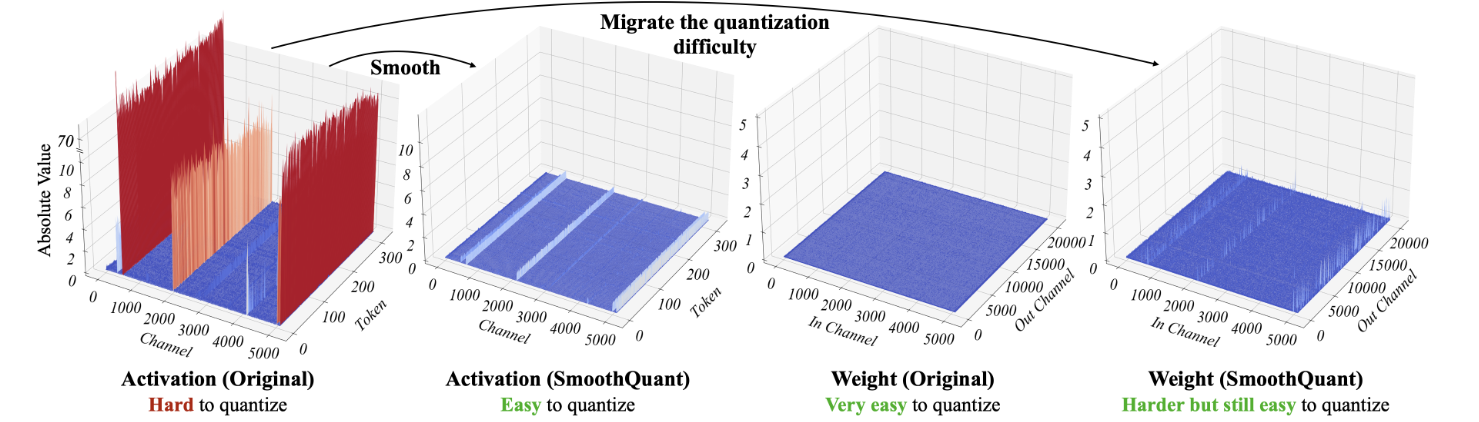
具体来说,就是先对X进行per-channel的scale,然后把scale因子乘回W,保证等价性。
值得注意的是,这里还不涉及量化阶段,只是前处理阶段,或者论文中提到的offline stage。
有些人可能好奇X/输入从哪里来,X是来自校准集的元素产生的activation,是用来确定s的。
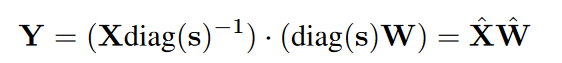
那么S应该怎么确定呢,如果要尽可能的处理X中的outlier,最好的方法就是每个通道除以该通道最大的ABS MAX。但是这么处理会导致W的outlier过大,W量化难度过大。所以综合考虑X/W的量化难度,s由下式决定,$\alpha$一般取0.5。
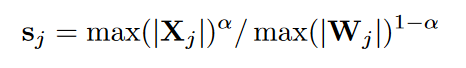
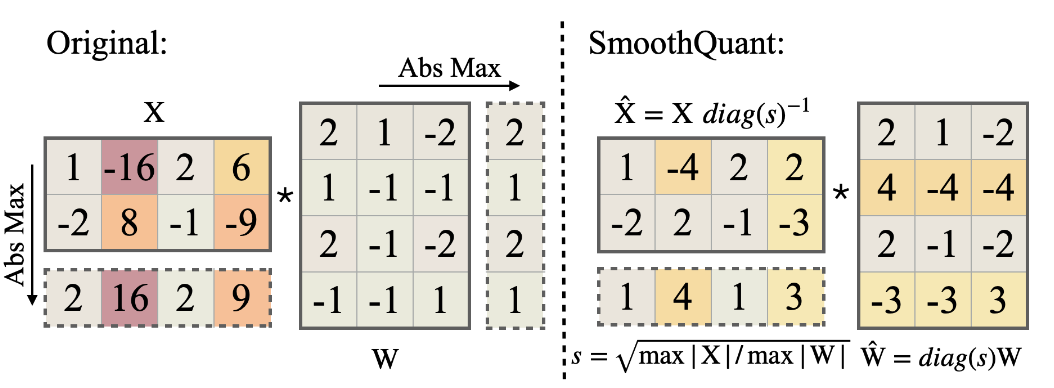
以下是一个Smooth例子,右侧是处理过的X/W。这个时候他们都比较好量化了。(后续实验好像是对这俩做了per-tensor量化)
再次重申,这个时候还没有到量化阶段,这只是对activation/weight进行smooth。接下来就可以拿着Smooth后的W去量化咯,这里直接采用常规量化就可以了。
可能有人好奇,推理的时候,activation每进行一个MM,都需要scale一下吗,其实这个$diag(s)^{-1}$可以融到之前一个操作的矩阵里,这样就避免了额外的延时。
AWQ: Activation-aware Weight Quantization
AWQ应该是目前最流行的INT4量化方法了,他是SmoothQuant的延申工作。
我们之前说到,LLM中有些activation的某些通道值特别大,导致其不好量化。而在仅权重量化的基础上,作者发现,如果保留这些通道对应的W的精度(这些salient weight大概占整个权重的0.1%),比如保持FP16,那么结果的ppl同样可以保持很好的性能。
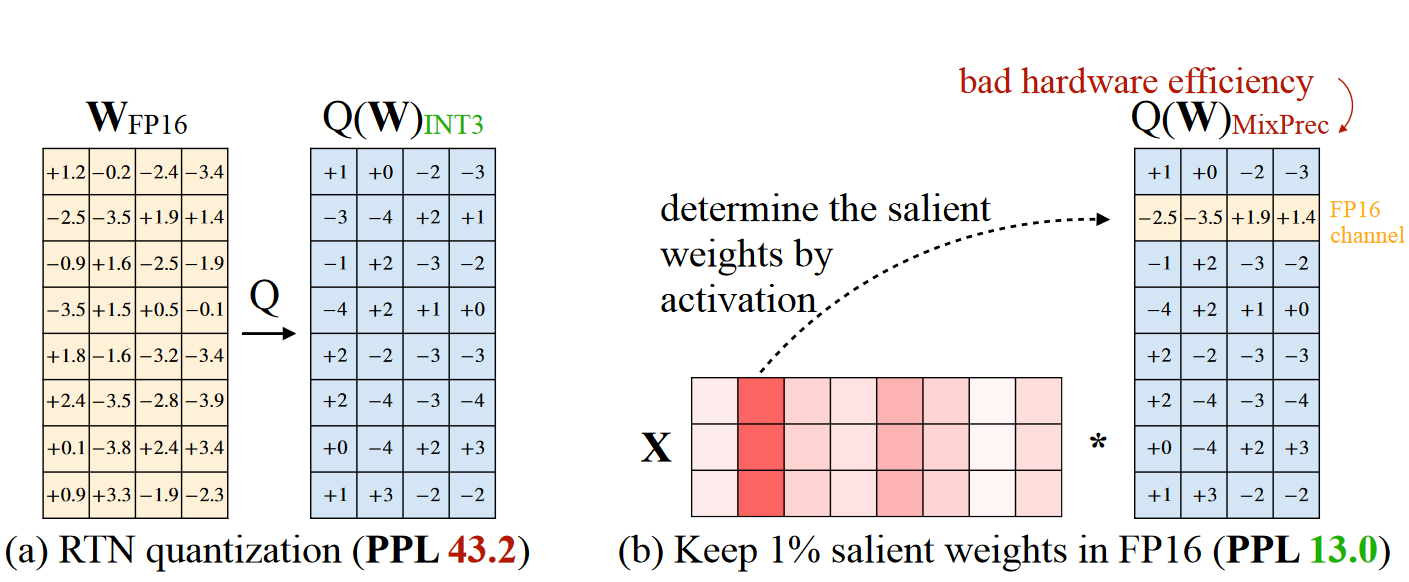
但是混合精度表示W对于并行是较差的,所以作者进一步提出Scale的操作,希望把这些salient weight也量化了。
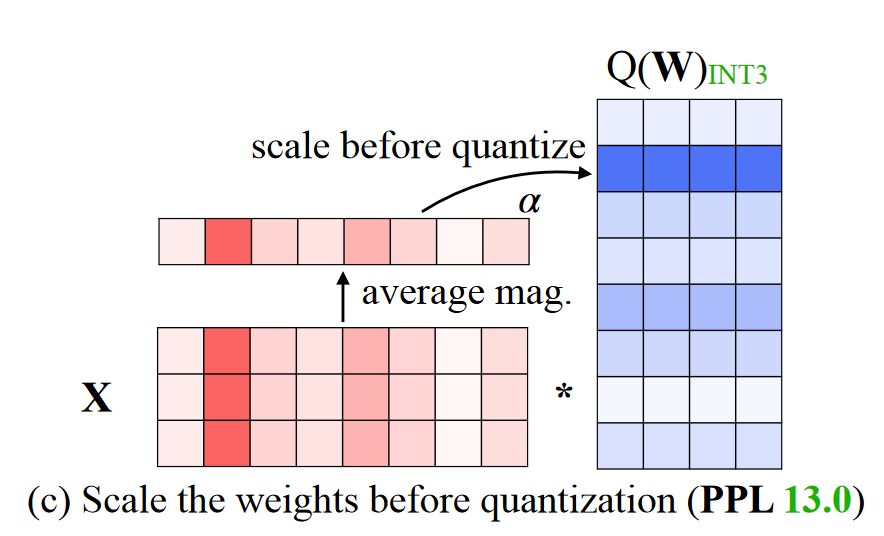
这一部分呢,我觉得跟SmoothQuant还是很像的,不过这里对于X的每个通道是计算平均值找到对应的salient weight。找到这些深蓝色的salient weight之后,作者对他们进行了一定的放缩,增大了W(对应的也要缩小X对应的channel,这个和SmoothQuant一样,当然看问题的角度不太一样,因为这里只考虑仅权重量化,并不量化activation)。
那么为什么做这个Scale操作呢?其实是为了减少量化损失,对于普通的权重量化,损失一般在于Round操作的舍入误差,一般浮点数的舍入值在0~0.5,平均误差就是0.25。
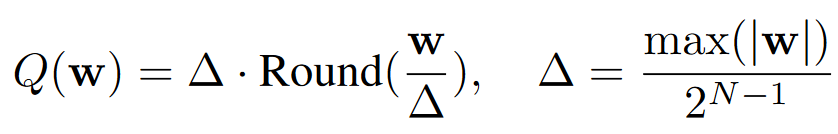
而先scale再量化的公式如下,一般来说在对应的salient weight row乘上因子s并不会影响weight的极值,那么$\Delta \approx \Delta'$,而Round误差一般也是不变的,那么下式的Err相比于原先的Err会多出一个$1/s(s \gt 1 )$,那么量化误差就变低。
这里的$\Delta$应该也是$\Delta'$,感觉是论文打错了,因为$\Delta$指$ws$即新权重的量化因子
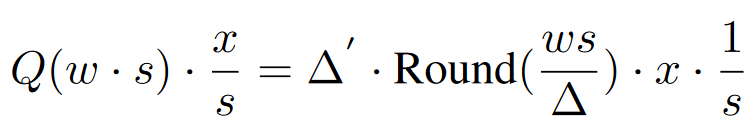
综上所述,对于salient weight对应的scale操作和SmoothQuant如出一辙,只不过一个是为了减少量化误差,一个是为了降低activation的量化难度。

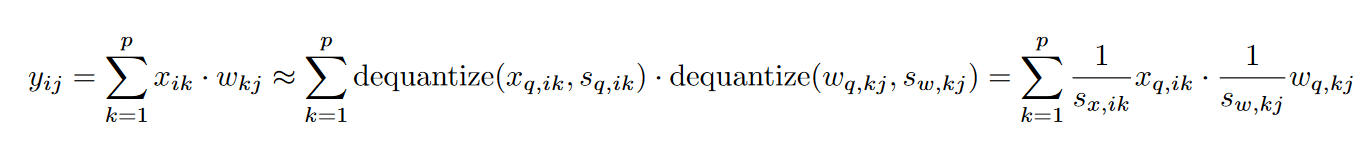
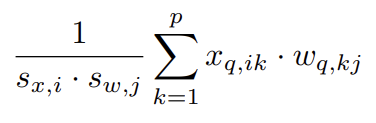
评论
一直都感觉这两篇的作坊很一样,当然讲故事的角度不一样
哈哈哈毕竟都是han lab做的