LoRA源码阅读

无 · 2023-12-20 · 804 人浏览
LoRA源码阅读

简单介绍LoRA，并对LoRA官方源码进行解读，修复了一个bug(可能)

Github: https://github.com/microsoft/LoRA

Arxiv: https://arxiv.org/abs/2106.09685

简单介绍

在LLM微调领域常常听到LoRA及其各种变体，一直以来的印象就是参数量少，不影响推理。今天彻底看看相应的论文和实现。

总结LoRA其实很容易，整篇论文除去实验，只需要一张图和一个公式。
$$
h = W_0x + \Delta Wx = W_0x + B A x \label{eq1} \tag{1}
$$

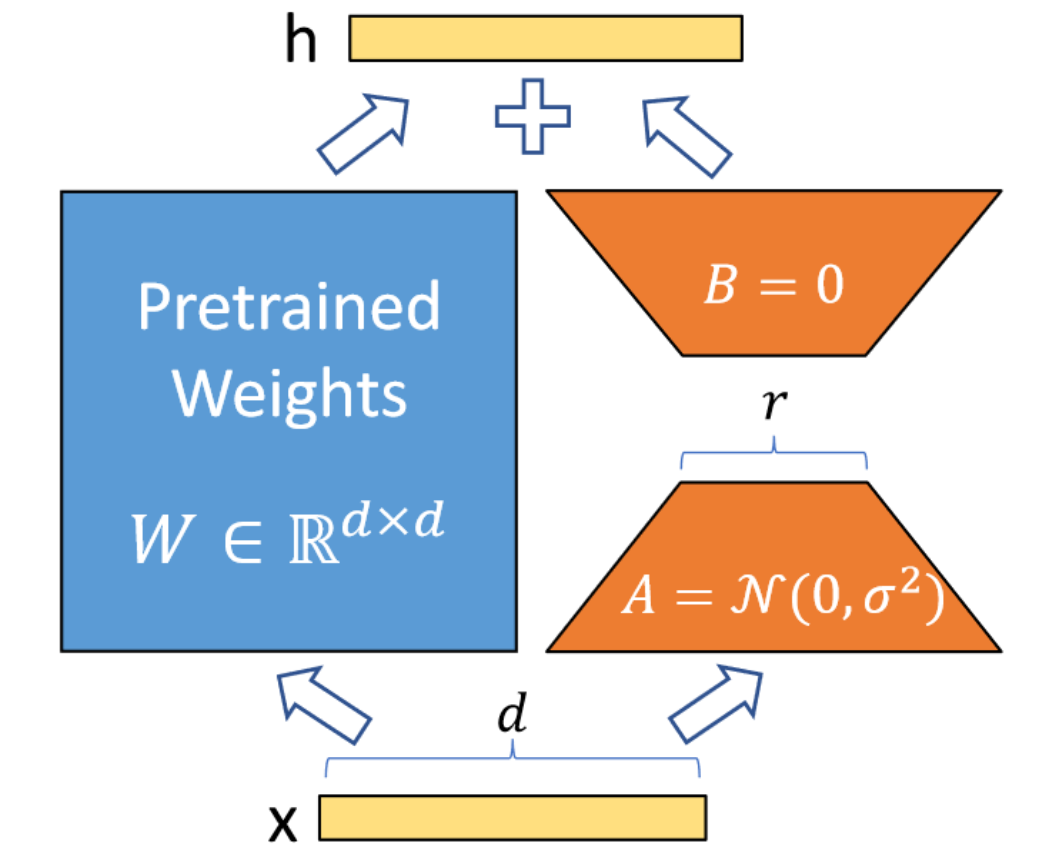
image-20231220195441669

简单来说，LoRA的灵感来自Aghajanyan等人1，他们发现预训练LLM具有较低的“instrisic dimension”，尽管随机投影到较小的子空间，但仍然可以有效地学习。

也就意味着式$\eqref{eq1}$中的$W$可能是低秩的，那么合理假设：在下游任务的微调过程中，模型权重改变量$\Delta W$也可能是低秩的，那么$\Delta W$就可以使用矩阵$A,B$进行建模。例如$A = matrix(d,r), B = matrix(r, h)$，两者的秩都不会超过$r$,且$r<<min(d,h)$。

这样的好处在于，由于$r$可以非常小(论文里甚至在训GPT-2时取$r=1$)，$A,B$的参数量相较于LLM也很小，微调友好。并且对于不同的下游任务，可以通过切换不同的$\Delta W$来实现task的切换(相当于复用预训练LLM的权重)。部署时，也可以将$\Delta W$合并到$W$中，从而不影响推理性能(与其他微调方法相比，如Adapter)。

源码解读

接下来直接看loralib的官方实现，整体代码还是十分简洁的。库里实现了nn.Embedding/nn.Linear/nn.Conv的LoRA封装。有些实现细节与论文有所出入，以下主要讨论出入部分。

LoRALayer

LoRALayer类的作用主要是定义LoRA中需要用到的一些参数，如rank，scale因子$\alpha$，dropout rate，以及参数是否合并的标志merge_weights等。

class LoRALayer():
    def __init__(
        self, 
        r: int, 
        lora_alpha: int, 
        lora_dropout: float,
        merge_weights: bool,
    ):
        self.r = r
        self.lora_alpha = lora_alpha
        # Optional dropout
        if lora_dropout > 0.:
            self.lora_dropout = nn.Dropout(p=lora_dropout)
        else:
            self.lora_dropout = lambda x: x
        # Mark the weight as unmerged
        self.merged = False
        self.merge_weights = merge_weights

Linear

先从Linear层说起，init函数中，定义了$A,B$两个矩阵。

这里A矩阵(B矩阵同理)定义成(r, in_features)的shape，而不是(in_features, r) , 应该是为了和nn.Linear.weight.data的shape: (out_features, in_features)保持一致

# Actual trainable parameters
if r > 0:
    self.lora_A = nn.Parameter(self.weight.new_zeros((r, in_features)))
    self.lora_B = nn.Parameter(self.weight.new_zeros((out_features, r)))

值得注意的是这里A矩阵使用的是kaiming_uniform_。

nn.init.kaiming_uniform_(self.lora_A, a=math.sqrt(5))
nn.init.zeros_(self.lora_B)

训练时，如果是train mode，会将$\Delta W$与$W$分离；如果是eval mode，则会将其合并，提高推理速度。这里的$\Delta W$就是$B @ A$。

def train(self, mode: bool = True):
    def T(w):
        return w.transpose(0, 1) if self.fan_in_fan_out else w
    nn.Linear.train(self, mode)
    if mode:
        if self.merge_weights and self.merged:
            # Make sure that the weights are not merged
            if self.r > 0:
                self.weight.data -= T(self.lora_B @ self.lora_A) * self.scaling
            self.merged = False
    else:
        if self.merge_weights and not self.merged:
            # Merge the weights and mark it
            if self.r > 0:
                self.weight.data += T(self.lora_B @ self.lora_A) * self.scaling
            self.merged = True

forward函数如下, 如果权重没有merge，分别计算结果相加即可。

def forward(self, x: torch.Tensor):
    def T(w):
        return w.transpose(0, 1) if self.fan_in_fan_out else w
    if self.r > 0 and not self.merged:
        result = F.linear(x, T(self.weight), bias=self.bias)            
        result += (self.lora_dropout(x) @ self.lora_A.transpose(0, 1) @ self.lora_B.transpose(0, 1)) * self.scaling
        return result
    else:
        return F.linear(x, T(self.weight), bias=self.bias)

Embedding

Embedding层与其他层不太一样，A矩阵的作用是为num_embeddings个值分配对应的向量，维度为r，B的作用是进一步将向量映射到embedding_dim维度。

这里A更合适的shape应该是(num_embeddings, r)，否则后续会出现很多transpose操作

这里这么写应该是和其他layer保持一致

self.lora_A = nn.Parameter(self.weight.new_zeros((r, num_embeddings)))
self.lora_B = nn.Parameter(self.weight.new_zeros((embedding_dim, r)))

因此初始化与论文的图不太一样，这里是将A矩阵置0。

nn.init.zeros_(self.lora_A)
nn.init.normal_(self.lora_B)

forward函数也是先通过A矩阵embedding到维度r，再和B矩阵相乘得到最后结果。

if self.r > 0 and not self.merged:
    result = nn.Embedding.forward(self, x)
    after_A = F.embedding(
        x, self.lora_A.transpose(0, 1), self.padding_idx, self.max_norm,
        self.norm_type, self.scale_grad_by_freq, self.sparse
    )
    result += (after_A @ self.lora_B.transpose(0, 1)) * self.scaling
    return result
else:
    return nn.Embedding.forward(self, x)

MergedLinear

这个类的作用主要是和Transformer的QKV结构适配，官方示例如下。

# ===== Before =====
# qkv_proj = nn.Linear(d_model, 3*d_model)
# ===== After =====
# Break it up (remember to modify the pretrained checkpoint accordingly)
q_proj = lora.Linear(d_model, d_model, r=8)
k_proj = nn.Linear(d_model, d_model)
v_proj = lora.Linear(d_model, d_model, r=8)
# Alternatively, use lora.MergedLinear (recommended)
qkv_proj = lora.MergedLinear(d_model, 3*d_model, r=8, enable_lora=[True, False, True])

大部分代码对于QKV的映射都是使用一个nn.Linear(d_model, 3*d_model)解决，但是LoRA有时候只想应用到QV上，这时候可以把Linear分成三个Linear，也可以使用MergedLinear。

MergedLinear实现其实有点像Bert里的Attention head pruning。lora_ind判断当前哪些输出需要用到LoRA，A矩阵是sum(enable_lora)个(r, in_features)矩阵，B矩阵是(out_features // len(enable_lora) * sum(enable_lora), r)的矩阵，这里对out_features进行了剪枝。

B矩阵其实也指后续AB合并用到的Conv1d.weight，shape为(final_out_features, in_channels/groups, kernel_size)

if r > 0 and any(enable_lora):
    self.lora_A = nn.Parameter(
    self.weight.new_zeros((r * sum(enable_lora), in_features)))
    self.lora_B = nn.Parameter(
    self.weight.new_zeros((out_features // len(enable_lora) * sum(enable_lora), r))
    ) # weights for Conv1D with groups=sum(enable_lora)
    self.scaling = self.lora_alpha / self.r
    # Freezing the pre-trained weight matrix
    self.weight.requires_grad = False
    # Compute the indices
    self.lora_ind = self.weight.new_zeros(
    (out_features, ), dtype=torch.bool
    ).view(len(enable_lora), -1)
    self.lora_ind[enable_lora, :] = True
    self.lora_ind = self.lora_ind.view(-1)

这里A、B矩阵的合并用到了1d卷积操作，具体shape可以见注释。groups的作用是对于不同输入(QKV)分别卷积。

def zero_pad(self, x):
    result = x.new_zeros((len(self.lora_ind), *x.shape[1:]))
    result[self.lora_ind] = x
    return result

def merge_AB(self):
    def T(w):
        return w.transpose(0, 1) if self.fan_in_fan_out else w
    delta_w = F.conv1d(
        self.lora_A.unsqueeze(0), # shape: [1, r * sum(enable_lora), in_features]
        self.lora_B.unsqueeze(-1), # shape: [out_features // len(enable_lora) * sum(enable_lora), r, 1]
        groups=sum(self.enable_lora)
    ).squeeze(0) # shape: [out_features // len(enable_lora) * sum(enable_lora), in_features]
    return T(self.zero_pad(delta_w)) # after zero_pad, shape: [out_features, in_features]

经过实测，这里的合并操作也可以写成以下形式，可能更方便理解

delta_w = (self.lora_B.view(sum(enable_lora), out_features//len(enable_lora), r) @ self.lora_A.view(sum(enable_lora), r, in_features)).view(-1,in_features)

ConvLoRA

ConvLoRA提供了1d/2d/3d卷积的封装，主要看AB矩阵的定义。这里的self.conv.groups与之前提到的一致，系卷积中的分组。

if r > 0:
    self.lora_A = nn.Parameter(
    self.conv.weight.new_zeros((r * kernel_size, in_channels * kernel_size))
)
    self.lora_B = nn.Parameter(
    self.conv.weight.new_zeros((out_channels//self.conv.groups*kernel_size, r*kernel_size))
)

AB矩阵的合并也很简单，直接(self.lora_B @ self.lora_A).view(self.conv.weight.shape)即可。

当然这里的问题在于(self.lora_B @ self.lora_A)的shape只能reshape到(out_channels, in_channels//self.conv.groups, kernel_size, kernel_size即2d卷积weight的shape。所以这种写法是否可以支持1d/3d，暂时打一个问号。

并且这里AB矩阵的rank最大可以是r * kernel_size，为什么不把kernel_size写到另外一边？

比如写成如下形式，正好也解决了Conv1d/3d的问题~

2023.12.20 Updates: Github上原来已经有这个问题的讨论了😀 https://github.com/microsoft/LoRA/issues/115

# Conv2d
self.lora_A = nn.Parameter(
    self.conv.weight.new_zeros((r, in_channels * kernel_size * kernel_size))
)
    self.lora_B = nn.Parameter(
    self.conv.weight.new_zeros((out_channels//self.conv.groups*kernel_size, r))
# Conv3d
self.lora_A = nn.Parameter(
    self.conv.weight.new_zeros((r, in_channels * kernel_size * kernel_size * kernel_size))
)
self.lora_B = nn.Parameter(
    self.conv.weight.new_zeros((out_channels//self.conv.groups*kernel_size, r))
# Conv1d
self.lora_A = nn.Parameter(
    self.conv.weight.new_zeros((r, in_channels * kernel_size))
)
self.lora_B = nn.Parameter(
    self.conv.weight.new_zeros((out_channels//self.conv.groups*kernel_size, r))

  1. http://arxiv.org/abs/2012.13255 ↩

LoRA LLM PEFT
2023 - 2024 Axuanz的学习日记. All Rights Reserved.
Theme Jasmine by Kent Liao